题目内容
(本题8分)
网上报道入春以来山东蔬菜严重滞销.为了减少菜农的损失,政府部门出台了相关补贴政策:采取每吨补贴0.02万元的办法补偿菜农.
下图是某菜农今年政府补助前、后蔬菜销售总收入y(万元)与销售量x(吨)的关系图.请结合图象解答以下问题:
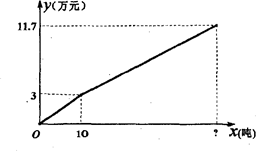
小题1:(1)在出台该项优惠政策前,蔬菜的售价为每吨多少万元?
小题2:(2)出台该项优惠政策后,该菜农将剩余蔬菜按原售价打九折赶紧全部销完,加上政府补贴共收入11.7万元,求菜农共销售了多少吨蔬菜?
小题3:(3)①求出台该项优惠政策后y与x的函数关系式;
②去年该菜农销售30吨,总收入为10.25万元;若按今年的销售方式,则至少要销售多少吨蔬菜,总收入才能达到或超过去年水平.
网上报道入春以来山东蔬菜严重滞销.为了减少菜农的损失,政府部门出台了相关补贴政策:采取每吨补贴0.02万元的办法补偿菜农.
下图是某菜农今年政府补助前、后蔬菜销售总收入y(万元)与销售量x(吨)的关系图.请结合图象解答以下问题:

小题1:(1)在出台该项优惠政策前,蔬菜的售价为每吨多少万元?
小题2:(2)出台该项优惠政策后,该菜农将剩余蔬菜按原售价打九折赶紧全部销完,加上政府补贴共收入11.7万元,求菜农共销售了多少吨蔬菜?
小题3:(3)①求出台该项优惠政策后y与x的函数关系式;
②去年该菜农销售30吨,总收入为10.25万元;若按今年的销售方式,则至少要销售多少吨蔬菜,总收入才能达到或超过去年水平.
小题1:(1)0.3
小题2:(2)40
小题3:(3)① y=0.27x+0.3 ② 35
分析:(1)(2)从函数图象容易看出前面一段是出台该项优惠政策前的情况,后面一段是出台该项优惠政策后的情况,前面一段所有的量已经知道,容易求出该果园共销售蔬菜的重量。(3)可根据图象的信息,先设出通式再利用待定系数法来确定y与x的函数关系式.然后根据函数的性质来判断出所求的方案。
解答:
(1)由图象知:每10吨收入3万元,
故每吨的蔬菜售价为:3/10=0.3万元
(2)设该菜农共销售x吨蔬菜,则:3+(0.3×90%+0.02)(x-10)=11.7
∴x=40(吨)。
答:菜农共销售40吨蔬菜。
(3)①设今年出台该项优惠政策后y与x的解析式为y=kx+b(k≠0)
由图象知:该图象过(10,3)和(40,11.7)两点.
故有:3=10k+b且11.7=40k+b;
∴k=0.29,b=0.1。
∴解析式为:y=0.29x+0.1(10≤x≤40)
②由题意知:y≥10.25
即:0.29x+0.1≥10.25
∴x≥35
故至少要销售35吨蔬菜,总收入才能达到或超过去年水平。
点评:本题主要考查了单价=总价÷数量的运用,待定系数法求函数的解析式的运用,及不等式的运用,在解答时求出一次函数的解析式是关键。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
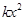 —x+1="0" 有两个不同的实数根,则k的范围是 ……( )
—x+1="0" 有两个不同的实数根,则k的范围是 ……( )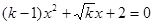 有实数根,则k应满足( )
有实数根,则k应满足( )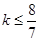
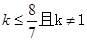
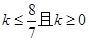
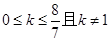
 中填上适当的数,使等式成立。
中填上适当的数,使等式成立。

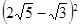
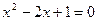
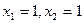
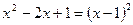
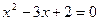

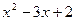
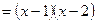
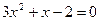
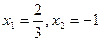
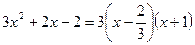
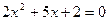
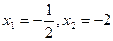
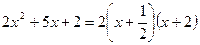
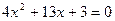
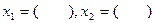
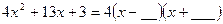
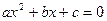 (
(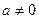 )有解为
)有解为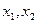 ,请你把二次三项式
,请你把二次三项式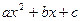 因式分解。
因式分解。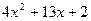 因式分解。
因式分解。