题目内容
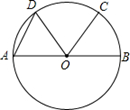
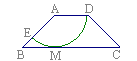
如图,已知AB=AC,∠BAC=120º,在BC上取一点O,以O为圆心OB为半径作圆,
①且⊙O过A点,过A作AD∥BC交⊙O于D,
求证:(1)AC是⊙O的切线;
(2)四边形BOAD是菱形。
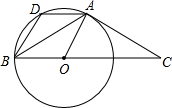
①且⊙O过A点,过A作AD∥BC交⊙O于D,
求证:(1)AC是⊙O的切线;
(2)四边形BOAD是菱形。

证明:(1)∵AB=AC,∠BAC=120º,∴∠ABC=∠C=30º。
∵OB=OA,∴∠BAO=∠ABC=30º。∴∠CAO=120º-30º=90º。
∴ OA⊥AC。
∵OA为⊙O的半径,∴ AC是⊙O的切线。
(2)连接OD,
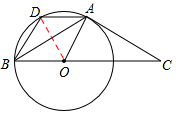
∵AD∥BC,
∴∠DAB=∠ABC=30º。
∴∠DAO=60º。
∵OA=OD,∴△OAD为等边三角形。
∴OB=OA=AD,
又∵AD∥BC,∴ADBO为平行四边形。
且OA=OB,∴四边形BOAD是菱形。
∵OB=OA,∴∠BAO=∠ABC=30º。∴∠CAO=120º-30º=90º。
∴ OA⊥AC。
∵OA为⊙O的半径,∴ AC是⊙O的切线。
(2)连接OD,

∵AD∥BC,
∴∠DAB=∠ABC=30º。
∴∠DAO=60º。
∵OA=OD,∴△OAD为等边三角形。
∴OB=OA=AD,
又∵AD∥BC,∴ADBO为平行四边形。
且OA=OB,∴四边形BOAD是菱形。
切线的判定,三角形内角和定理,等腰三角形的性质,平行线的性质,菱形的判定。
【分析】(1)求证AC是⊙O的切线,则证OA⊥AC,很显然要运用圆的切线的判定定理。
(2)要证四边形BOAD是菱形,先证BOAD为平行四边形,再证一组邻边相等。
【分析】(1)求证AC是⊙O的切线,则证OA⊥AC,很显然要运用圆的切线的判定定理。
(2)要证四边形BOAD是菱形,先证BOAD为平行四边形,再证一组邻边相等。

练习册系列答案
相关题目

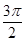
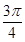
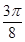
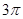
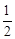 ,母线长为2,它的侧面展开图的圆心角是 ▲ .
,母线长为2,它的侧面展开图的圆心角是 ▲ .