题目内容
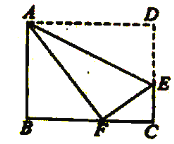
【题目】如图，在△ABC中，点O是AC边上一动点，过点O作BC的平行线交∠ACB的角平分线于点E，交∠ACB的外角平分线于点F
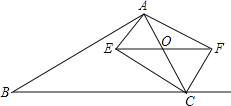
（1）求证：EO＝FO；
（2）当点O运动到何处时，四边形CEAF是矩形？请证明你的结论．
（3）在第（2）问的结论下，若AE＝3，EC＝4，AB＝12，BC＝13，请直接写出凹四边形ABCE的面积为 ．
【答案】（1）详见解析；（2）当点O运动到AC的中点时，四边形CEAF是矩形，理由详见解析；（3）24．
【解析】
（1）由平行线的性质和角平分线的定义得出∠OEC＝∠OCE，证出EO＝CO，同理得出FO＝CO，即可得出EO＝FO；
（2）由对角线互相平分证明四边形CEAF是平行四边形，再由对角线相等即可得出结论；
（3）先根据勾股定理求出AC，得出△ACE的面积＝
AE×EC，再由勾股定理的逆定理证明△ABC是直角三角形，得出△ABC的面积＝ABAC，凹四边形ABCE的面积＝△ABC的面积﹣△ACE的面积，即可得出结果．
（1）证明：∵EF∥BC，
∴∠OEC＝∠BCE，
∵CE平分∠ACB，
∴∠BCE＝∠OCE，
∴∠OEC＝∠OCE，
∴EO＝CO，
同理：FO＝CO，
∴EO＝FO；
（2）解：当点O运动到AC的中点时，四边形CEAF是矩形；理由如下：
由（1）得：EO＝FO，
又∵O是AC的中点，
∴AO＝CO，
∴四边形CEAF是平行四边形，
∵EO＝FO＝CO，
∴EO＝FO＝AO＝CO，
∴EF＝AC，
∴四边形CEAF是矩形；
（3）解：由（2）得：四边形CEAF是矩形，
∴∠AEC＝90°，
∴AC＝
＝
＝5，
△ACE的面积＝AE×EC＝×3×4＝6，
∵122+52＝132，
即AB2+AC2＝BC2，
∴△ABC是直角三角形，∠BAC＝90°，
∴△ABC的面积＝ABAC＝×12×5＝30，
∴凹四边形ABCE的面积＝△ABC的面积﹣△ACE的面积＝30﹣6＝24；
故答案为：24．
