题目内容
【题目】（10分）如图，已知AB∥CD，分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系，并从所得的四个关系中任选一个加以说明，证明所探究的结论的正确性。
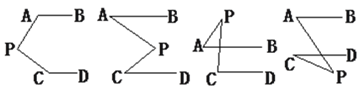
结论⑴____________________⑵___________________
⑶__________________⑷___________________
选择结论____，说明理由是什么。
【答案】 ∠APC+∠PAB+∠PCD=360° ∠APC=∠PAB+∠PCD ∠APC=∠PCD-∠PAB ∠APC=∠PAB-∠PCD (2)理由见解析
【解析】理由如下：
过P点作PQ∥AB
∵AB∥CD，PQ∥AB
∴PQ∥CD
∴∠QPC=∠C
∵PQ∥AB
∴∠QPA=∠A,
∵∠APC=∠APQ+∠QPC
∴∠APC=∠A+∠C
练习册系列答案
相关题目
