Question

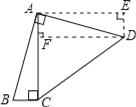
【题目】如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（　　）

A. y= B. y= C. y= D. y=

Answer 1

【答案】C

【解析】作AE⊥AC，DE⊥AE，两线交于E点，作DF⊥AC垂足为F点，

∵∠BAD=∠CAE=90°，即∠BAC+∠CAD=∠CAD+∠DAE，∴∠BAC=∠DAE

又∵AB=AD，∠ACB=∠E=90°，

∴△ABC≌△ADE（AAS），

∴BC=DE，AC=AE，

设BC=a，则DE=a，DF=AE=AC=4BC=4a，

CF=AC﹣AF=AC﹣DE=3a，

在Rt△CDF中，由勾股定理得，

CF2+DF2=CD2，即（3a）2+（4a）2=x2，

解得：a=，

∴y=S四边形ABCD=S梯形ACDE=×（DE+AC）×DF=×（a+4a）×4a=10a2=x2，

故选C．