题目内容
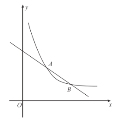
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在原点的左侧,点
在原点的左侧,点![]() 在原点的右侧),与
在原点的右侧),与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
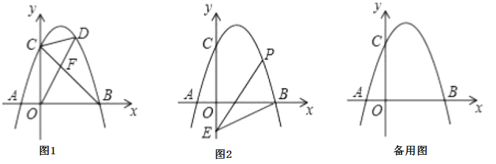
(1)求该抛物线的函数解析式.
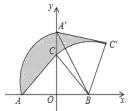
(2)如图1,连接![]() ,点
,点![]() 是直线
是直线![]() 上方抛物线上的点,连接
上方抛物线上的点,连接![]() ,
,![]() .
.![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是抛物线上的点,连接
是抛物线上的点,连接![]() ,
,![]() ,
,![]() 形成的
形成的![]() 中,是否存在点
中,是否存在点![]() ,使
,使![]() 或
或![]() 等于
等于![]() ?若存在,请直接写出符合条件的点
?若存在,请直接写出符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 、
、![]() 、
、![]() 、
、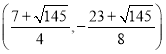
【解析】
(1)![]() ,则:
,则:![]() ,
,![]() ,把
,把![]() 、
、![]() 坐标代入抛物线解析式,利用待定系数法可求得抛物线解析式;
坐标代入抛物线解析式,利用待定系数法可求得抛物线解析式;
(2)![]() ,则
,则![]() ,即:
,即:![]() ,即可求解;
,即可求解;
(3)分![]() 或
或![]() 等于
等于![]() 两种情况分别求解即可.
两种情况分别求解即可.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
把![]() 、
、![]() 坐标代入抛物线得:
坐标代入抛物线得:![]()
解得:![]()
∴抛物线解析式为:![]()
(2)∵![]() ,∴
,∴![]() ,即,
,即,
设:![]() 点横坐标为
点横坐标为![]() ,则
,则![]() 点横坐标为
点横坐标为![]() ,点
,点![]() 在直线
在直线![]() 上,
上,
求得![]() 所在的直线表达式为:
所在的直线表达式为:![]() ,则
,则![]() ,
,
由可求得点![]() ,
,
把![]() 点坐标代入抛物线的解析式,解得:
点坐标代入抛物线的解析式,解得:![]() 或
或![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
(3)①当![]() 时,
时,
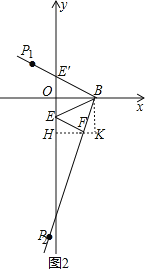
当![]() 在
在![]() 轴上方时,
轴上方时,
如图2,设![]() 交
交![]() 轴于点
轴于点![]() ,
,
![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,
![]() △
△![]() ,
,
![]() ,
,![]() 点
点![]() ,
,
直线![]() 过点
过点![]() 、
、![]() ,则其解析式为:
,则其解析式为:![]() ,
,
解方程组 得:
得:![]() (不合题意,舍去)或
(不合题意,舍去)或 ,
,
故点![]() 的坐标为: (
的坐标为: (![]() );
);
当![]() 在
在![]() 轴下方时,
轴下方时,
如图2,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
直线![]() 可以看成直线
可以看成直线![]() 平移而得,其
平移而得,其![]() 值为
值为![]() ,
,
则其直线表达式为:![]() ,
,
设点![]() ,过点
,过点![]() 作
作![]() 轴交于点
轴交于点![]() ,作
,作![]() 于点
于点![]() ,
,
则点![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
即:![]() ,
,
解得:![]() ,则点
,则点![]() ,
,
则直线![]() 的表达式为:
的表达式为:![]() ,
,
解方程组 得:
得:![]() (不合题意,舍去)或
(不合题意,舍去)或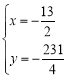 ,
,
故点![]() 的坐标为:
的坐标为: ![]() ;
;
②当![]() 时,
时,

当![]() 在
在![]() 上方时,如图3,点
上方时,如图3,点![]() 为图2所求,
为图2所求,
设![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
由①知,直线![]() 的表达式为:
的表达式为:![]() ,
,
设点![]() ,
,![]() ,
,
由![]() ,同理可得:
,同理可得:![]() ,
,
故点![]() ,则直线
,则直线![]() 的表达式为:
的表达式为:![]() ,
,
解方程组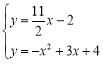
得:![]() (不合题意,舍去)或
(不合题意,舍去)或 ,
,
故点![]() 的坐标为:
的坐标为: ![]() ;
;
当![]() 在
在![]() 下方时,
下方时,
同理可得:![]() (舍去负值),
(舍去负值),
故点![]() .
.
故点![]() 的坐标为:
的坐标为:![]() 、
、![]() 、
、![]() 、
、 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某单位现要组织其市场和生产部的员工游览该公园,门票价格如下:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
如果按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1245元;如果两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为945元.那么该公司这两个部的人数之差的绝对值为_____.