题目内容
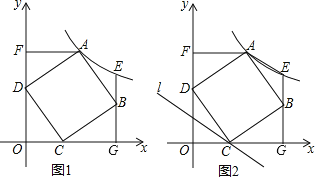
【题目】如图1，在平面直角坐标系中，正方形ABCD顶点C（3，0），顶点D（0，4），过点A作AF⊥y轴于F点，过点B作x轴的垂线交过A点的反比例函数y＝
（k＞0）的图象于E点，交x轴于G点．
（1）求证：△CDO≌△DAF．
（2）求反比例函数解析式及点E的坐标；
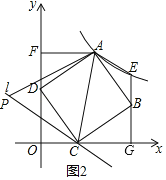
（3）如图2，过点C作直线l∥AE，在直线l上是否存在一点P使△PAC是等腰三角形？若存在，求P点坐标，不存在说明理由．
【答案】（1）见解析；（2）为y＝
，点E的坐标为（7，4）；（3）在直线l上存在一点P使△PAC是等腰三角形，点P的坐标为（﹣3，6），（﹣2，5），（8，﹣5），（﹣
，
）．
【解析】
（1）利用同角的余角相等可得出∠CDO＝∠DAF，结合∠DOC＝∠AFD＝90°及DC＝AD，可证出△CDO≌△DAF；
（2）利用全等三角形的性质可求出AF，FD的长，进而可得出点A的坐标，由点A的坐标，利用反比例函数图象上点的坐标特征可求出反比例函数解析式，同（1）可证出△CDO≌△BCG，利用全等三角形的性质及反比例函数图象上点的坐标特征可求出点E的坐标；
（3）由点A，E的坐标，利用待定系数法可求出直线AE的解析式，结合直线l∥AE及点C的坐标可求出直线l的解析式，设点P的坐标为（m，﹣m+3），结合点A，C的坐标可得出AC2，AP2，CP2的值，分AC＝AP，CA＝CP及PA＝PC三种情况可得出关于m的方程，解之即可得出点P的坐标．
（1）证明：∵四边形ABCD为正方形，
∴AD＝DC，∠ADC＝90°，
∴∠ADF+∠CDO＝90°．
∵∠ADF+∠DAF＝90°，
∴∠CDO＝∠DAF．
在△CDO和△DAF中，
，
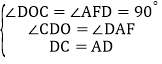∴△CDO和△DAF（AAS）．
（2）解：∵点C的坐标为（3，0），点D的坐标为（0，4），
∴OC＝3，OD＝4．
∵△CDO和△DAF，
∴FA＝OD＝4，FD＝OC＝3，
∴OF＝OD+FD＝7，
∴点A的坐标为（4，7）．
∵反比例函数y＝
（k＞0）过点A，
∴k＝4×7＝28，
∴反比例函数解析式为y＝．
同（1）可证出：△CDO≌△BCG，
∴GB＝OC＝3，GC＝OD＝4，
∴OG＝OC+GC＝7，
∴点G的坐标为（7，0）．
当x＝7时，y＝
＝4，
∴点E的坐标为（7，4）．
（3）解：设直线AE的解析式为y＝ax+b（a≠0），
将A（4，7），E（7，4）代入y＝ax+b，得：
，
解得：
，
∴直线AE的解析式为y＝﹣x+11．
∵直线l∥AE，且直线l过点C（3，0），
∴直线l的解析式为y＝﹣x+3．
设点P的坐标为（m，﹣m+3），
∵点A的坐标为（4，7），点C的坐标为（3，0），
∴AP2＝（m﹣4）2+（﹣m+3﹣7）2＝2m2+32，AC2＝（3﹣4）2+（0﹣7）2＝50，CP2＝（m﹣3）2+（﹣m+3）2＝2m2﹣12m+18．
分三种情况考虑：
①当AC＝AP时，50＝2m2+32，
解得：m1＝3（舍去），m2＝﹣3，
∴点P的坐标为（﹣3，6）；
②当CA＝CP时，50＝2m2﹣12m+18，
解得：m3＝﹣2，m4＝8，
∴点P的坐标为（﹣2，5）或（8，﹣5）；
③当PA＝PC时，2m2+32＝2m2﹣12m+18，
解得：m＝﹣，
∴点P的坐标为（﹣，）．
综上所述：在直线l上存在一点P使△PAC是等腰三角形，点P的坐标为（﹣3，6），（﹣2，5），（8，﹣5），（﹣，）．
