题目内容
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2),现将△ABC平移,使点A变换为点A',点B'、C'分别是B、C的对应点.
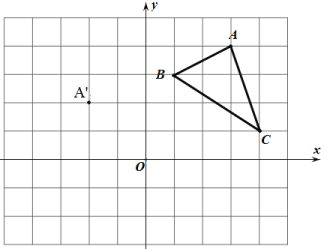
(1)直接写出点B'、C'的坐标:B' ,C' ;并在坐标系中画出平移后的△A'B'C'(不写画法);
(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P的坐标是 ;
(3)若△ABC绕点C逆时针旋转90°至△A1B1C,画出△A1B1C.
(4)求△A'B'C'的面积是多少?
【答案】(1)B'(-4,1)C'(-1,-1),见解析;(2)(a-5,b-2);(3)见解析;(4)3.5
【解析】
(1)根据平面直角坐标系写出点B′、C′的坐标即可;根据网格结构找出点B′、C′的位置,然后顺次连接即可;
(2)根据平移规律写出即可;
(3)根据旋转的性质,即可画出旋转后的图形;
(4)根据三角形面积等于正方形面积减去三个小三角形面积解答即可.
解:(1)根据平移的规则,得:B′(-4,1)、C′(-1,-1);△A′B′C′如图所示;

(2)∵点A(3,4)、A′(-2,2),
∴平移规律为向左平移5个单位,向下平移2个单位,
∴P(a,b)平移后的对应点P′的坐标是:(a-5,b-2).
故答案为:(-4,1);(-1,-1);(a-5,b-2).
(3)∵△ABC绕点C逆时针旋转90°至△A1B1C,则上图所示;
(4)△A′B′C′的面积=3×3![]() ×2×1
×2×1![]() ×3×1
×3×1![]() ×2×3=3.5;
×2×3=3.5;

【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
数据段 | 频数 | 频率 |
30~40 | 10 | 0.05 |
40~50 | 36 | |
50~60 | 0.39 | |
60~70 | ||
70~80 | 20 | 0.10 |
总计 | 200 | 1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;

(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?



