Question

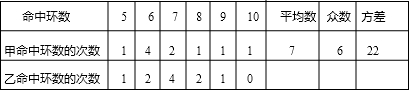
甲、乙两名学生进行射击练习，两人在相同条件下各射击10次，其结果统计如下：

命中环数	5	6	7	8	9	10
甲命中环数的次数	1	4	2	1	1	1
乙命中环数的次数	1	2	4	2	1	0

（1）根据表中的相关数据，计算甲乙两人命中环数的平均数、众数、方差．
（2）根据所学的统计知识，利用上述数据评价甲乙两人的射击水平．

Answer 1

分析：（1）根据平均数、众数和方差的定义分别求出乙的三个量．
（2）从集中趋势和稳定性两个方面来考查两人的成绩．

解答：解：（1）甲学生相关的数据为：
平均数为：（5×1+6×4+7×2+8×1+9×1+10×1）÷10=7；
众数为：6；
方差为：

S

2 甲

=

1

n

[（x₁-

.

x

）²+（x₂-

.

x

）²+…+（x_n-

.

x

）²]
=

1

10

[（5-7）²+（6-7）²+…+（10-7）²]
=2.2．

乙学生相关的数据为：
平均数为：（5×1+6×2+7×4+8×2+9×1）÷10=7；
众数为7；
方差为：

S

2 乙

=

1

n

[（x₁-

.

x

）²+（x₂-

.

x

）²+…+（x_n-

.

x

）²]
=

1

10

[（5-7）²+（6-7）²+…+（9-7）²]
=1.2．

（2）从平均水平看，甲、乙两名学生射击的环数平均数均为7环，水平相当；
从集中趋势看，乙的众数比甲大，乙的成绩比甲的好些；
从稳定性看，s_甲²＞s_乙²，所以乙的成绩比甲稳定．

点评：此题主要考查了方差与平均数和众数的求法，训练学生对平均数，众数，方差的理解及运用能力，熟练记忆方差公式是解题关键．