题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 交y轴于点B(0,3),交x轴于A,C两点,C点坐标(4,0),点P是BC上方抛物线上一动点(P不与B,C重合).
交y轴于点B(0,3),交x轴于A,C两点,C点坐标(4,0),点P是BC上方抛物线上一动点(P不与B,C重合).
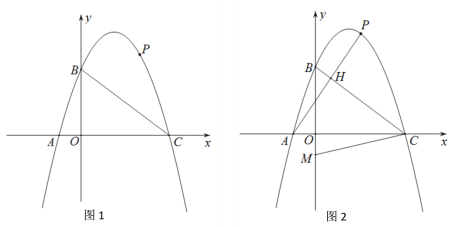
(1)求抛物线的解析式;
(2)若点P到直线BC距离是![]() ,求点P的坐标;
,求点P的坐标;
(3)连接AP交线段BC于点H,点M是y轴负半轴上一点,且CH=BM,当AH+CM的值最小时,请直接写出点M的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)点M坐标(0,
;(3)点M坐标(0,![]() ).
).
【解析】
(1)将点B(4,0),C(0,3)代入原方程得出b、c的值即可求得;
(2)过点P作PE⊥BC于E,则PE=![]() ,过点P作PG∥BC于G,则PG=
,过点P作PG∥BC于G,则PG=![]() ,设P点坐标为
,设P点坐标为![]() ,则G点坐标为
,则G点坐标为![]() ,即PG=
,即PG=![]() ,整理得,
,整理得,![]() ,解得
,解得![]() 或
或![]() ,即可求得点P的坐标;
,即可求得点P的坐标;
(3)在Rt△BOC中,∠BOC=90°,可得BC=5,过点C作CH⊥x轴于N,使CN=BC;连接AN交BC于H交抛物线于点P,则点P即为所求,在射线CB上截取CH=BM,因为CN∥y轴,可得∠NCH=∠CBM,又因为CN=BC,可证△BMC≌△CHN(SAS),即可得到HN=CM,AH+CM=AH+NH,所以当A,N,H三点共线时点P即为所求,AH+CM最小,设AH表达式为![]() ,把A(-1,0),N(4,5)代入上式,求得解析式为y=x+1,联立方程组
,把A(-1,0),N(4,5)代入上式,求得解析式为y=x+1,联立方程组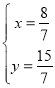 ,解得
,解得![]() ,得到H点坐标是(
,得到H点坐标是(![]() ),CH=BM=
),CH=BM=![]() ,即可得到点M坐标为(0,
,即可得到点M坐标为(0,![]() );
);
(1)把B(4,0),C(0,3)代入原方程得,![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)过点P作PE⊥BC于E,则PE=![]() ,
,
过点P作PG∥BC于G,则PG= ,
,
设P点坐标为![]() ,则G点坐标为
,则G点坐标为![]() ,
,
∴PG=![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ,
,
∴P![]() ;
;
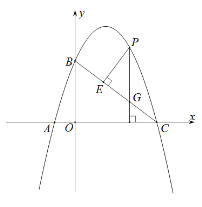
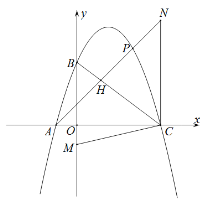
(3)∵在Rt△BOC中,∠BOC=90°,
∴BC=![]() ,
,
过点C作CH⊥x轴于N,使CN=BC;连接AN交BC于H交抛物线于点P,则点P即为所求,
在射线CB上截取CH=BM,
∵CN∥y轴,
∴∠NCH=∠CBM,
∵CN=BC,
∴△BMC≌△CHN(SAS),
∴HN=CM,
∴AH+CM=AH+NH,
∴当A,N,H三点共线时点P即为所求,AH+CM最小,
设AH表达式为![]() ,
,
把A(-1,0),N(4,5)代入上式,
![]() ,
,
解得![]() ,
,
∴y=x+1,
联立方程组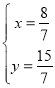
解得![]() ,
,
∴H点坐标是(![]() ),CH=BM=
),CH=BM=![]() ,
,
点M坐标(0,![]() );
);