题目内容
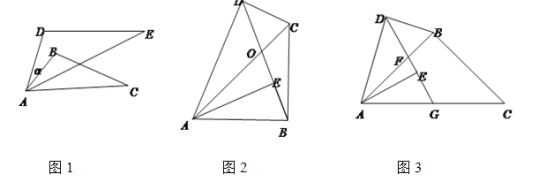
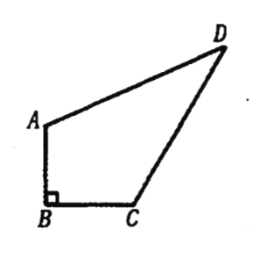
【题目】探究:如图①, ![]() ,试说明
,试说明![]() .下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
.下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
解: ∵![]() .(已知)
.(已知)
∴ ![]() .( )
.( )
同理可证, ![]() .
.
∵ ![]() ,
,
∴![]() .( )
.( )
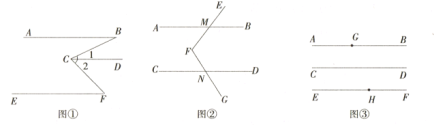
应用:如图②, ![]() ,点
,点![]() 在
在![]() 之间,
之间,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为_____________度.
的大小为_____________度.
拓展:如图③,直线![]() 在直线
在直线![]() 之间,且
之间,且![]() ,点
,点![]() 分别在直线
分别在直线![]() 上,点
上,点![]() 是直线
是直线![]() 上的一个动点,且不在直线
上的一个动点,且不在直线![]() 上,连结
上,连结![]() .若
.若![]() ,则
,则![]() =________度.
=________度.
【答案】探究:两直线平行,内错角相等;等量代换;应用:60;拓展:70或290.
【解析】
探究:利用平行线的性质解决问题即可;
应用:利用探究中的结论解决问题即可;
拓展:分两种情形,画出图形分别求解即可.
解:探究::∵AB∥CD,
∴∠B=∠1(两直线平行,内错角相等),
同理可证,∠F=∠2,
∵∠BCF=∠1+∠2,
∴∠BCF=∠B+∠F.(等量代换),
故答案为:两直线平行,内错角相等;等量代换.
应用:由探究可知:∠EFG=∠AMF+∠CNF,
∵∠EFG=115°,∠AMF=∠EMB=55°,
∴∠DNG=∠CNF=∠EFG-∠AMF=115°55°=60°,
故答案为:60;
拓展:如图,
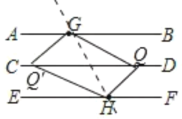
当点Q在直线GH的右侧时,
∠AGQ+∠EHQ,
=180°-∠BGQ+180°-∠FHQ,
=360°-(∠BGQ+∠FHQ),
=360°-∠GQH,
=360°70°,
=290°,
当点Q′在直线GH的左侧时,∠AGQ′+∠EHQ′=∠GQ′H=70°,
故答案为:70或290.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目