题目内容
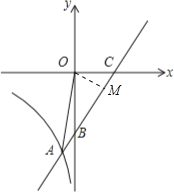
【题目】直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=![]() (x<0)交于点A(﹣1,n).
(x<0)交于点A(﹣1,n).
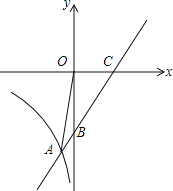
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
【答案】(1)直线与双曲线的解析式分别为y=x﹣4,y=![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据待定系数法,可得直线解析式,根据自变量与函数值的对应关系,可得A点坐标,再根据待定系数法,可得答案;
(2)根据等腰直角三角形的判定,可得△OCB是等腰直角三角形,根据正弦函数,可得OM的长,根据勾股定理,可得OA的长,再根据锐角三角函数的定义,可得答案.
解:(1)将C点代入y=x+b中得到b=﹣4,
∴y=x﹣4;
再将A点带入y=x﹣4得到n=﹣5,
∴A(﹣1,﹣5),
∴m=﹣1×(﹣5)=5,
∴y=![]()
∴直线与双曲线的解析式分别为y=x﹣4,y=![]() ;
;
(2)过点O作OM⊥AC于点M,
当x=0时,y=﹣4,即B(0,﹣4).
∵OC=OB=4,
∴△OCB是等腰直角三角形,
∴∠OBC=∠OCB=45°
∴在△OMB中 sin45°=![]() ,
,
∴OM=4×![]() =2
=2![]() .
.
∴在直角三角形AOM中,
AO=![]() =
=![]() ,
,
sin∠OAB=![]() =
=![]() .
.

练习册系列答案
相关题目