题目内容
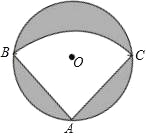
【题目】如图，AB是⊙O的直径，点C在⊙O上，D是
中点，若∠BAC=70°，求∠C．
下面是小雯的解法，请帮他补充完整．
解：在⊙O中，
∵D是的中点
∴
=
，
∴∠l=∠2（ ）（填推理的依据）
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径，
∴∠ADB=90°（ ）（填推理的依据）
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上，
∴∠C+∠B=180°（ ）（填推理的依据）
∴∠C=l80°﹣∠B= （填计算结果）
【答案】等弧所对的圆周角相等；直径所对的圆周角是直角；圆内接四边形的对角互补；125°；
【解析】
根据圆周角定理，圆内接四边形的性质，求出∠B即可解决问题；
在⊙O中，
∵D是
的中点
∴
=
，
∴∠l=∠2（等弧所对的圆周角相等）
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径，
∴∠ADB=90°（直径所对的圆周角是直角）
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上，
∴∠C+∠B=180°（圆内接四边形的对角互补）
∴∠C=l80°﹣∠B=125°
故答案是：等弧所对的圆周角相等，直径所对的圆周角是直角，圆内接四边形的对角互补，125°．
练习册系列答案
中考解读考点精练系列答案
相关题目
