题目内容
【题目】如图![]() ,在
,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
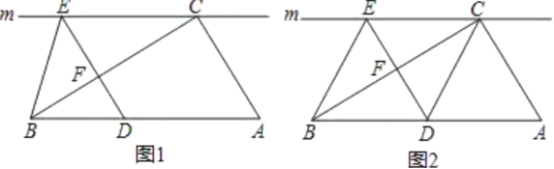
(1)求证:![]() ;
;
(2)如图![]() ,当点
,当点![]() 是
是![]() 中点时,连接
中点时,连接![]() .
.
①四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
②当![]()
![]() 时,四边形
时,四边形![]() 是正方形.(直接写出答案)
是正方形.(直接写出答案)
【答案】(1)见解析;(2)①菱形,理由见解析;②![]() .
.
【解析】
(1)证明DE∥AC,利用平行四边形的判定和性质得结论;
(2)①先证明四边形BECD是平行四边形,再利用直角三角形斜边的中线等于斜边的一半说明邻边相等,证明该四边形是菱形;
②由菱形、正方形、平行四边形的性质可得结论.
(1)∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,![]() .
.
∴四边形![]() 为平行四边形
为平行四边形
∴![]() .
.
(2)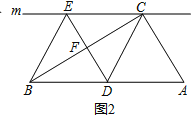
①四边形BECD是菱形.
∵由(Ⅰ)知:四边形DECA是平行四边形,
∴CE=DA,CE∥AD
在Rt△ABC中,∵点D是AB的中点,
∴BD=DC=DA,
∴四边形BECD是菱形.
②当∠A=45°时,
由于四边形DECA是平行四边形,
∴∠EDB=∠A=45°,
又∵BE=BD,
∴∠BED=∠EDB=45°,
∴∠EBD=90°.
由于四边形BECD是菱形,
∴四边形BECD是正方形.
故答案为:45°

练习册系列答案
相关题目
【题目】学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,下表记录了A、B、C三名学生的得分情况,则参赛学生D的得分可能是( )
参赛学生 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 14 | 6 | 64 |
A.66B.93C.40D.87