��Ŀ����
����Ŀ���Ķ����ϣ�
�������Ǻ����������µĹ�ʽ��
Sin(��![]() ��)=sin��cos��
��)=sin��cos��![]() cos��sin��
cos��sin��
tan(��![]() ��)=
��)=![]()
������Щ��ʽ���Խ�һЩ��������ǵ����Ǻ���ת��Ϊ����ǵ����Ǻ�������ֵ��
����tan15��=tan(45��-30��)
=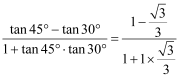
=![]()
=![]()
���������Ķ����ϣ���ѡ���ʵ��Ĺ�ʽ������������
��1������sin15��
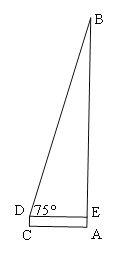
��2��������������һ�ƶ���˾���ź�����С����������ѧ����ѧ֪ʶ�����������ĸ߶ȣ�С��վ��������A����7����C�����������������Ϊ75����С�����۾������ľ���DCΪ1.62���������С��������ź����ĸ߶ȡ�����ȷ��0.1�����ο����ݣ�![]() ��
��
���𰸡���1��![]() ����2��ԼΪ27.7�ף�
����2��ԼΪ27.7�ף�
��������
�����������1����15����Ϊ45��-30���Ժ������ù�ʽsin����������=sin��cos�¡�cosasin�����㣬�������sin15����ֵ��
��2���ȸ���������Ǻ����Ķ������BE�ij����ٸ���AB=AE+BE���ɵó����ۣ�
�����������1��sin15��=sin��45��-30����=sin45��cos30��-cos45��sin30��=![]() ��
��
��2����Rt��BDE�У��ߡ�BED=90������BDE=75����DE=AC=7�ף�
��BE=DE��tan��BDE=DE��tan75����
��tan75��=tan��45��+30����=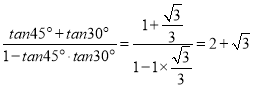 ��
��
��BE=7��2+![]() ��=14+7
��=14+7![]() ��
��
��AB=AE+BE=1.62+14+7![]() ��27.7��������
��27.7��������
���ź����ĸ߶�ԼΪ27.7�ף�