题目内容
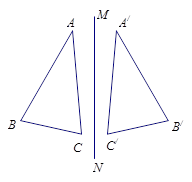
如图,在矩形ABCD中,AB=3,BC=4,将其折叠,使AB边落在对角线AC上,得到折痕AE,则点E到点B的距离为


| A.3/2 | B.2 | C.5/2 | D. 3 |
A
试题分析:由于AE是折痕,可得到AB=AF,BE=EF,设出未知数,在Rt△EFC中利用勾股定理列出方程,通过解方程即可得到答案.
设BE=x,
∵AE为折痕,
∴AB=AF,BE=EF=x,∠AFE=∠B=90°,
Rt△ABC中,
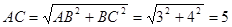 ,
,∴Rt△EFC中,FC=5-3=2,EC=4-X,
∴
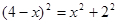 ,
,解得
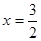 ,
,故选A.
点评:熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.

练习册系列答案
相关题目
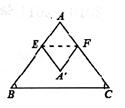
 中,已知
中,已知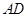 =8,折叠纸片使
=8,折叠纸片使 边与对角线
边与对角线 重合,点
重合,点 落在点
落在点 处,折痕为
处,折痕为 ,且
,且 =3,则
=3,则
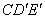 (使
(使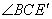 <180°),连接
<180°),连接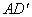 、
、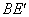 ,设直线
,设直线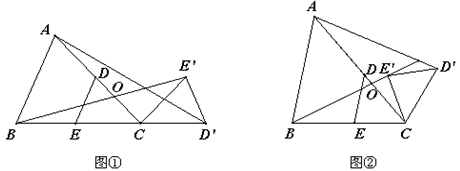

 ,0)绕着原点顺时针方向旋转45°角得到点B,则点B的坐标 是 .
,0)绕着原点顺时针方向旋转45°角得到点B,则点B的坐标 是 .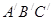 关于MN对称,并且AB=5,BC=3,则
关于MN对称,并且AB=5,BC=3,则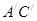 的取值范围是 .
的取值范围是 .