题目内容
阅读下面材料:
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.对于平面图形A,如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖.
例如:图中①的三角形被一个圆覆盖,②中的四边形被两个圆所覆盖.
回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是______cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是______cm;
(3)长为2cm,宽为1cm的矩形被两个半径均为r的圆所覆盖,r的最小值是______cm.这两个圆的圆心距是______cm
解:(1)以正方形的对角线为直径做圆是覆盖正方形的最小圆,半径r的最小值= ;
;
(2)边长为1 cm的等边三角形被一个半径为r的圆所覆盖,这个最小的圆是正三角形的外接圆,如图作三角形ABC的高AD构成直角三角形ABD,斜边AB=1,BD= ,
,
因为三角形是正三角形,
所以∠ABC=60°,O是外心,所以∠OBC=30°,OD= OB,
OB,
设OA=OB=x,则OD= x,
x,
在直角三角形OBD中,根据勾股定理列方程:x2=( )2+(
)2+( x)2,
x)2,
解得:x= .
.

(3)如图:矩形ABCD中AB=1,BC=2,则覆盖ABCD的两个圆与矩形交于E、F两点,由对称性知E、F分别是AD和BC的中点,则四边形ABFE、EFCD是两个边长为1的正方形,所以圆的半径r= ,两圆心距=1.
,两圆心距=1.
分析:当一个图形被一个圆覆盖时,当圆是这个图形的外接圆时,圆最小;当矩形被两圆覆盖,圆最小时,两圆的公共弦一定是1cm,则每个圆内的部分是一个边长是1的正方形.
点评:正确理解什么情况下圆最小是解决本题的关键.
 ;
;(2)边长为1 cm的等边三角形被一个半径为r的圆所覆盖,这个最小的圆是正三角形的外接圆,如图作三角形ABC的高AD构成直角三角形ABD,斜边AB=1,BD=
 ,
,因为三角形是正三角形,
所以∠ABC=60°,O是外心,所以∠OBC=30°,OD=
 OB,
OB,设OA=OB=x,则OD=
 x,
x,在直角三角形OBD中,根据勾股定理列方程:x2=(
 )2+(
)2+( x)2,
x)2,解得:x=
 .
.
(3)如图:矩形ABCD中AB=1,BC=2,则覆盖ABCD的两个圆与矩形交于E、F两点,由对称性知E、F分别是AD和BC的中点,则四边形ABFE、EFCD是两个边长为1的正方形,所以圆的半径r=
 ,两圆心距=1.
,两圆心距=1.分析:当一个图形被一个圆覆盖时,当圆是这个图形的外接圆时,圆最小;当矩形被两圆覆盖,圆最小时,两圆的公共弦一定是1cm,则每个圆内的部分是一个边长是1的正方形.
点评:正确理解什么情况下圆最小是解决本题的关键.

练习册系列答案
相关题目
 一水库的水位在最近5小时之内持续上涨,下表记录了这5个小时水位高度.
一水库的水位在最近5小时之内持续上涨,下表记录了这5个小时水位高度.
| t/时 | 0 | 1 | 2 | 3 | 4 | 5 |
| y/米 | 10 | 10.05 | 10.10 | 10.15 | 10.20 | 10.25 |
(2)据估计按这种上涨规律还会持续若干个小时,请预测再过多少小时水位高度将达到10.35米?
 如图,梯形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥BD于P,已知AD:BC=3:4,则BD:AC的值是________.
如图,梯形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥BD于P,已知AD:BC=3:4,则BD:AC的值是________. ;②
;②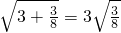 ;
; ;④
;④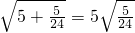
 如图,两条抛物线
如图,两条抛物线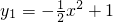 ,
,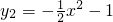 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为________.
与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为________.