题目内容
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+
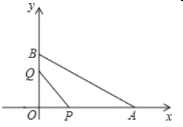
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
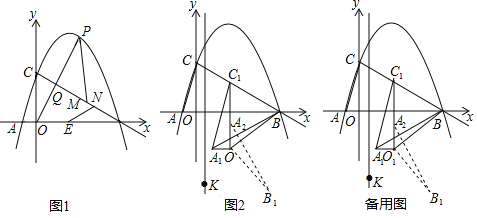
(1)如图1,当![]() 值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
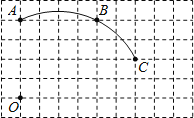
(2)如图2,连接AC,将△AOC沿射线CB方向平移,点A,C,O平移后的对应点分别记作A1,C1,O1,当C1B=O1B时,连接A1B、O1B,将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=![]() 上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
【答案】(1)![]() ;(2)K1(
;(2)K1(![]() ,
,![]() ),K2(
),K2(![]() ,-2),K3(
,-2),K3(![]() ,-5),K4(
,-5),K4(![]() ,
,![]() )
)
【解析】
(1)先求出抛物线与坐标轴的交点坐标,待定系数法求出直线BC解析式,过P作PT∥y轴交BC于T,构造△PTQ∽△ACQ,设点P的横坐标为m,通过相似三角形性质得出![]() 关于m的函数表达式,利用二次函数最值即可;
关于m的函数表达式,利用二次函数最值即可;
(2)存在.先求出△AOC沿射线CB方向平移,并能使C1B=O1B时△A1O1B各顶点的坐标,在求出△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1的各顶点坐标,最后按照△A2B1K为等腰三角形进行分类讨论即可.
解:(1)在抛物线y=-![]() x2+
x2+![]() x+3中,令x=0,得y=3,∴C(0,3);
x+3中,令x=0,得y=3,∴C(0,3);
令y=0,得-![]() x2+
x2+![]() x+3=0,解得:x1=-1,x2=4,∴B(4,0)
x+3=0,解得:x1=-1,x2=4,∴B(4,0)
设直线BC解析式为y=kx+b,将B(4,0),C(0,3);代入并解得:k=![]() ,b=3
,b=3
∴直线BC解析式为y=![]() x+3;
x+3;
过P作PT∥y轴交BC于T,设P(t,![]() +
+![]() +3),则T(t,
+3),则T(t,![]() +3),如图所示:
+3),如图所示:

∴PT=(![]() +
+![]() +3)-(
+3)-(![]() +3)=
+3)=![]() +3t,OC=3;
+3t,OC=3;
∵PT∥y轴
∴△PTQ∽△ACQ
∴![]() =
=![]() =
=![]() +t=
+t=![]()
∴当t=2时,![]() 值最大;此时,P(2,
值最大;此时,P(2,![]() ),PT=3;
),PT=3;
在Rt△BOC中,BC=![]() =5,
=5,
∴当NE⊥BC时,NE=![]() BE,此时,NE-
BE,此时,NE-![]() BE=0最小,
BE=0最小,
∵MN=1,∴PM+MN的最小值即PM最小值
∴PM⊥BC时,PM最小
过P作PM⊥BC于M,∴∠PMT=∠BOC=90°
∵∠PTM=∠BCO
∴![]() =
=![]()
∴PM=![]() PT=
PT=![]() ,
,
故PM+MN+NE-![]() BE的最小值=
BE的最小值=![]() ;
;
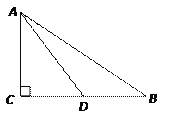
(2)存在.在△AOC中,∠AOC=90°,OA=1,OC=3,∴AC=![]()
如图2,
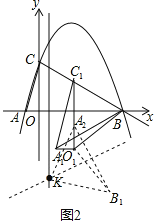
由平移得:C1O1=OC=3,A1O1=OA=1,A1C1=AC=![]() ,
,
∵C1B=O1B,C1O1⊥OB
∴C1G=![]() C1O1=
C1O1=![]()
∴BG=2,OG=2
∴C1(2,![]() ),O1(2,
),O1(2,![]() ),A1(1,
),A1(1,![]() );
);
∴C1B=O1B=![]() ,A1B=
,A1B=![]() =
=![]() ;
;
∵△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1,
∴A2O1=1,O1B1=![]() ,A2B1=
,A2B1=![]() ;
;
∴A2(2,![]() ),B1(
),B1(![]() ,
,![]() )
)
∵△A2B1K为等腰三角形,
∴A2K=B1K或A2B1=B1K或A2K=A2B1,
设K(![]() ,m)
,m)
①当A2K=B1K时,则:![]() +
+![]() =
=![]() +
+![]() ,解得:m=-
,解得:m=-![]() ,∴K1(
,∴K1(![]() ,
,![]() ),
),
②当A2B1=B1K时,则:![]() +
+![]() =
=![]() ,解得:m1=-2,m2=-5,∴K2(
,解得:m1=-2,m2=-5,∴K2(![]() ,-2),K3(
,-2),K3(![]() ,-5),
,-5),
③当A2K=A2B1时,则:![]() +
+![]() =
=![]() ,解得:m1=
,解得:m1=![]() (舍),m2=
(舍),m2=![]() ,∴K4(
,∴K4(![]() ,
,![]() );
);
综上所述,点K的坐标为:K1(![]() ,
,![]() ),K2(
),K2(![]() ,-2),K3(
,-2),K3(![]() ,-5),K4(
,-5),K4(![]() ,
,![]() ).
).

【题目】近一周,各个学校均在紧张有序的进行中考模拟考试,学生们通过模拟考试来调整自己的状态并了解自己的学业水平.某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数,在全年级随机抽取了男、女各40名学生的成绩,并将数据进行整理分析,给出了下面部分信息:
①男生成绩扇形统计图和女生成绩频数分布直方图如下:(数据分组为A组:x<50,B组:50≤x<60,C组:60≤x<70,D组:70≤x≤80)
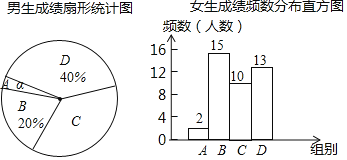
②男生C组中全部15名学生的成绩为:63,69,64,62,68,69,65,69,65,66,67,61,67,66,69
③两组数据的平均数、中位数、众数、满分率、极差(单位:分)如表所示:
平均数 | 中位数 | 众数 | 满分率 | 极差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
(1)扇形统计图A组学生对应的圆心角α的度数为______.
(2)若成绩在70分(包含70分)以上为优秀,请你估计该校1200名学生此次考试中优秀的人数.