题目内容
【题目】如图,△ADF≌△CBE,且点E,B,D,F在一条直线上.试判断:
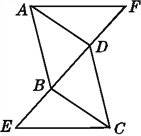
(1)AD与BC的位置关系(并加以说明);
(2)BF与DE的数量关系,并说明理由.
【答案】(1)AD∥BC；(2)BF=DE
【解析】试题分析：（1）由“已知全等三角形的对应角相等”推知∠ADF=∠CBE，则等角的补角相等，即内错角∠ADB=∠CBD，则易证得AD∥BC；
（2）由“已知全等三角形的对应边相等”推知BE=DF，则根据等式的性质得到BE+BD=DF+BD，即BF=DE．
试题解析: (1)AD∥BC.理由如下：
∵△ADF≌△CBE，
∴∠ADF=∠CBE，
∴∠ADB=∠CBD，
∴AD∥BC；
(2)BF=DE.理由如下：
∵△ADF≌△CBE，
∴BE=DF，
∴BE+BD=DF+BD，即BF=DE.
练习册系列答案
阅读快车系列答案
相关题目
