题目内容
【题目】在平面直角坐标系中,点A、B、C的坐标分别为![]() 、
、![]() 、
、![]() ,点E是
,点E是![]() 的外接圆上一点,BE交线段AC于点D,若
的外接圆上一点,BE交线段AC于点D,若![]() ,则点D的坐标为______.
,则点D的坐标为______.
【答案】![]()
【解析】
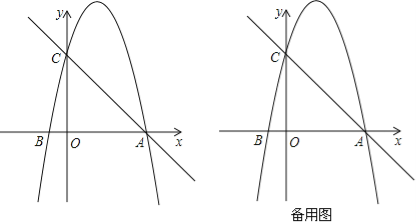
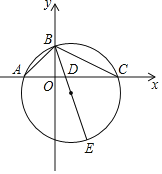
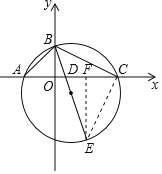
连接CE,过E作EF⊥AC于F,根据已知条件得到OA=OB=2,OC=4,得到△OBA是等腰直角三角形,得到∠BAC=45°,根据圆周角定理得到∠BEC=∠BAC=45°,推出△BCE是等腰直角三角形,求得BC=CE,根据全等三角形的性质得到E(2,﹣4),待定系数法得到直线BE的解析式为y=﹣3x+2,于是得到结论.
连接CE,过E作EF⊥AC于F.
∵点A、B、C的坐标分别为(﹣2,0)、(0,2)、(4,0),∴OA=OB=2,OC=4,∴△OBA是等腰直角三角形,∴∠BAC=45°,∴∠BEC=∠BAC=45°.
∵∠DBC=45°,∴∠BCE=90°,∴△BCE是等腰直角三角形,∴BC=CE.
∵∠CBO+∠BCO=∠BOC+∠ECF=90°,∴∠OBC=∠FCE.
在△OBC与△FCE中,∵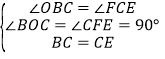 ,∴△OBC≌△FCE(AAS),∴CF=OB=2,EF=OC=4,∴OF=2,∴E(2,﹣4),设直线BE的解析式为y=kx+b,∴
,∴△OBC≌△FCE(AAS),∴CF=OB=2,EF=OC=4,∴OF=2,∴E(2,﹣4),设直线BE的解析式为y=kx+b,∴![]() ,∴
,∴![]() ,∴直线BE的解析式为y=﹣3x+2,当y=0时,x
,∴直线BE的解析式为y=﹣3x+2,当y=0时,x![]() ,∴D(
,∴D(![]() ,0).
,0).
故答案为:(![]() ,0).
,0).

练习册系列答案
相关题目