题目内容
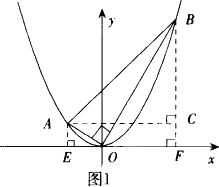
已知抛物线y=ax2(a>0)上有A、B两点,它们的横坐标分别为-1,2.又知△AOB是直角三角形,求a的值.
答案:
解析:
解析:
|
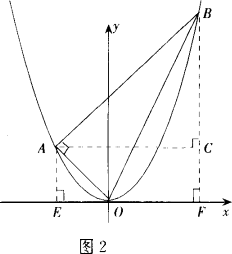
分析:因题目未指明哪个角是直角,应分情况进行讨论. (2)设∠OAB=90°(图2). 作AE⊥x轴于E,BF⊥x轴于F,AC⊥BF于C. 同(1)求得OA2=a2+1,OB2=16a2+4, 在Rt△AOB中, ∵OB2-OA2=AB2, ∴16a2+4―a2―1=AB2,即AB2=15a2+3. ① 在Rt△ABC中,有 AB2=AC2+BC2=9+(3a)2=9a+9. ② 由于①、②得 15a2+3=9a+9. 解得 a=1(舍去负值). (3)设∠OBA=90°(图3). 作AE⊥x轴于E,BF⊥x轴于F,BC⊥AE于C. 同(1)求得OA2=a2+4,OB2=16a2+4, ∴AB2=OA2-OB2=a2+4-16a2-4=-15a2-3<0, ∴这样的线段AB不存在. 综上,符合条件的a的值为 图形间的位置关系不确定导致求解时需周全考虑各种情况,按各种情况分别求解,不要以偏概全. |

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目


 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.

 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;