题目内容
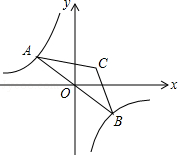
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数![]() 的图像相交于点
的图像相交于点![]() 和点
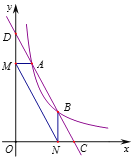
和点![]() ,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 与四边形MNCA的周长相等;④
与四边形MNCA的周长相等;④![]() .其中正确的个数是( )个.
.其中正确的个数是( )个.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】根据待定系数法求出直线和反比例函数的解析式,得到CD点的坐标,由此求出DM、AM、CN、NB的长,然后根据SAS得到![]() ,然后根据M、N的求出MN的解析式,从而判断②,再根据①的结论和周长判断出③,最后根据三角形的面积判断④.
,然后根据M、N的求出MN的解析式,从而判断②,再根据①的结论和周长判断出③,最后根据三角形的面积判断④.
∵直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数![]() 的图像相交于点
的图像相交于点![]() 和点
和点![]()
∴一次函数的解析式为y=-2x+5,反比例函数的解析式为:y=![]()
∴C点为(![]() ,0),D点为(0,5)
,0),D点为(0,5)
∴DM=2,AM=1,CN=1,NB=2
∵AM⊥y轴,BN⊥x轴
∴![]() ,
,
故①正确;
由M(0,3),N(![]() ,0),求得MN的解析式为:y=-2x+3,
,0),求得MN的解析式为:y=-2x+3,
∴![]() ,故②正确;
,故②正确;
∵四边形![]() 的周长=BA+AD+DM+MN+NB=(BA+AD+MN)+DM+NB=(BA+AD+MN)+4
的周长=BA+AD+DM+MN+NB=(BA+AD+MN)+DM+NB=(BA+AD+MN)+4
四边形MNCA的周长=AM+AB+BC+MN+NC=(BA+BC+MN)+AM+NC=(BA+AD+MN)+2
∴四边形![]() 与四边形MNCA的周长不相等
与四边形MNCA的周长不相等
故③不正确;
由OD=5,AM=1,可得![]() =
=![]() ,由OC=
,由OC=![]() ,NB=2,可得
,NB=2,可得![]() =
=![]() =
=![]() ,可知
,可知![]() ,故④正确.
,故④正确.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目