题目内容
【题目】如图①,先把一矩形ABCD纸片上下对折,设折痕为MN;如图②,再把点B 叠在折痕线MN上,得到Rt△ABE.过B点作PQ⊥AD,分别交BC、AD于点P、Q.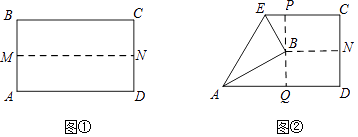
(1)求证:△PBE∽△QAB;
(2)在图②中,EB是否平分∠AEC?请说明理由;
(3)在(1)(2)的条件下,若AB=4,求PE的长度.
【答案】
(1)
解:在矩形ABCD中
∵EC∥AD,又PQ⊥AD
∴PQ⊥EC,
∴∠EPB=∠BQA=90°,
∴∠BAQ+∠ABQ=90°
∵是把B点叠在MN上得到△ABE
∴∠ABE=90°
∴∠EBP+∠ABQ=90°
∴∠EBP=∠BAQ
∴△PBE∽△QAB
(2)
解:解:EB平分∠AEC,
理由如下:
∵△PBE∽△QAB,
∴ ![]()
∵由折叠可知BQ=PB.
∴ ![]() 即
即 ![]() ,
,
又∵∠ABE=∠BPE=90°,
∴△PBE∽△BAE.
∴∠AEB=∠PEB,
∴EB平分∠AEC
(3)
解:∵PQ=AB=4,
∴PB=BQ=2,
在Rt△QAB中,AB=4,BQ=2,
∴AQ= ![]() =2
=2 ![]()
∵△PBE∽△QAB,
∴ ![]() ,
,
∴ ![]() ,
,
∴PE= ![]()
【解析】(1)先利用互余得出∠EBP=∠BAQ,进而得出结论;(2)由(1)的结论△PBE∽△QAB,得出 ![]() 即
即 ![]() ,进而判断出△PBE∽△BAE.即可得出∠AEB=∠PEB,结论得证;(3)先用勾股定理求出AQ,进而借助(1)的结论即可求出PE.
,进而判断出△PBE∽△BAE.即可得出∠AEB=∠PEB,结论得证;(3)先用勾股定理求出AQ,进而借助(1)的结论即可求出PE.
【考点精析】本题主要考查了角平分线的性质定理和相似三角形的判定的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案



