Question

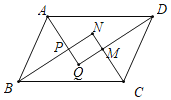
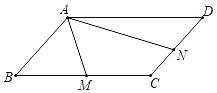
【题目】如图，平行四边形ABCD中，M，N分别为边BC，CD的中点，且∠MAN＝∠ABC，则的值是______．

Answer 1

【答案】

【解析】

延长AM与DC的延长线交于点E，先证明△ABM≌△ECM，得AM与AE的关系，AB与EN和ED的关系，再证明△EAN∽△EDA，由相似三角形比例线段便可得结论．

解：延长AM与DC的延长线交于点E，

∵四边形ABCD为平行四边形，

∴AB＝CD，AB//CD，∠B＝∠D，

∵∠B＝∠MAN，

∴∠ECM＝∠B＝∠MAN＝∠D，

∵M是BC的中点，N是CD的中点，

∴BM＝CM，CN＝DN＝，

在△ABM和△ECM中，

，

∴△ABM≌△ECM（ASA），

∴AB＝CE，AM＝EM，

∴AE＝2AM，EN＝AB，ED＝2AB，

∵∠EAN＝∠D，∠E＝∠E，

∴△EAN∽△EDA，

∴，即EA2＝EDEN，

∴，

∴，

∴．

故答案为：．