题目内容
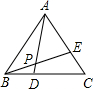如图，等边△ABC，D、E分别在BC、AC上，且CD=AE，AD、BE相交于点P，试求∠BPD的度数．
解：∵CD=AE，∴BD=CE，
在△ABD和△BCE中，
，
∴△ABD≌△BCE，
故∠BAD=∠CBE，
∵∠APE=∠ABE+∠BAD，∠APE=∠BPD，∠ABE+∠CBE=60°，
∴∠BPD=∠APE=∠ABC=60°，
∠BPD的度数为60°．
分析：易证△ABD≌△BCE，可得∠BAD=∠CBE，根据∠APE=∠ABE+∠BAD，∠APE=∠BPD，∠ABE+∠CBE=60°，即可求得∠APE=∠ABC，即可解题．
点评：本题考查了等边三角形各内角为60°的性质，考查了全等三角形的证明，考查了全等三角形对应角相等的性质，本题中求证∠APE=∠ABC是解题的关键．
在△ABD和△BCE中，
，∴△ABD≌△BCE，
故∠BAD=∠CBE，
∵∠APE=∠ABE+∠BAD，∠APE=∠BPD，∠ABE+∠CBE=60°，
∴∠BPD=∠APE=∠ABC=60°，
∠BPD的度数为60°．
分析：易证△ABD≌△BCE，可得∠BAD=∠CBE，根据∠APE=∠ABE+∠BAD，∠APE=∠BPD，∠ABE+∠CBE=60°，即可求得∠APE=∠ABC，即可解题．
点评：本题考查了等边三角形各内角为60°的性质，考查了全等三角形的证明，考查了全等三角形对应角相等的性质，本题中求证∠APE=∠ABC是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
8、如图，等边△ABC中，D为BC上一点，△ABD经过旋转后到达△ACE的位置，如果∠BAD=18°，则旋转角等于（ ）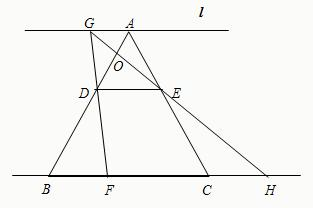
已知：如图，等边△ABC的边长为6，点D、E分别在AB、AC上，且AD=AE=2，直线l过点A，且l∥BC，若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动，设F点运动的时间为t秒，当t＞0时，直线DF交l于点G，GE的延长线与BC的延长线交于点H，AB与GH相交于点O．
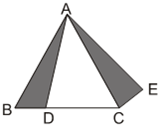
（2013•黔东南州一模）如图，等边△ABC的面积为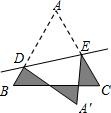
如图，等边△ABC的边长为1cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为（ ）