Question

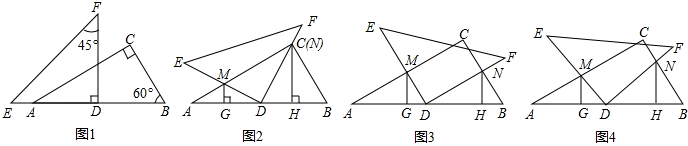
已知：将一副三角板(Rt△ABC和Rt△DEF)如图①摆放，点E、A、D、B在一条直线上，且D是AB的中点。将Rt△DEF绕点D顺时针方向旋转角α(0°＜α＜90°)，在旋转过程中，直线DE、AC相交于点M，直线DF、BC相交于点N，分别过点M、N作直线AB的垂线，垂足为G、H.
【小题1】当α＝30°时，DF刚好过点C(如图②)，求证：AM=DM；
【小题2】在（1）的条件下，试判断线段AG与DH的数量关系，并说明理由；
【小题3】“当在Rt△DEF绕点D顺时针方向旋转过程中时α=60°(如图③)，(2)中的结论是否成立？

Answer 1

【小题1】证明：∵∠A=30°，α＝30°
∴∠MDA=∠A=30°
∴ AM="DM "
（1）      【小题2】结论：AG="DH                     "
理由：∵D是AB的中点
∴AD="BD                 "
∵AM=DM，MG⊥AD
∴AG=             
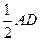
∵∠CDB=180°-∠EDF-∠MDA=60°
∴∠CDB=∠B=60°
∴ND=NB

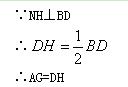
【小题3】

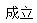
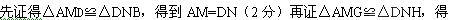
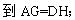解析:
p;【解析】略