题目内容
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,点E、F、G分别在AB、BC、CD上,且AE=GF=GC.
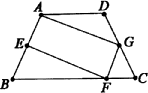
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC=2∠EFB时,求证:四边形AEFG是矩形.
答案:
解析:
解析:
|
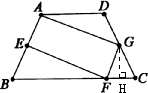
(1)∵在梯形ABCD中,AB=DC ∴∠B=∠C ∵GF=GC ∴∠C=∠GFC ∴∠B=∠GFC ∴AB∥GF,即AE∥GF 3分 又AE=GF ∴四边形AEFG是平行四边形 5分 (2)过点G作GH⊥FC,垂足为H 6分 ∵GF=GC ∴∠FGH= ∵∠FGC=2∠EFB ∴∠FGH=∠EFB ∵∠FGH+∠GFH=90° ∴∠EFB+∠GFH=90° 8分 ∴∠EFG=90° ∵四边形AEFG是平行四边形 ∴四边形AEFG是矩形 10分
|

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S. 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,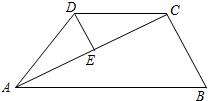 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=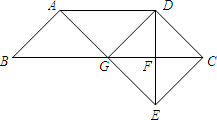 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.