题目内容
在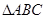 中,
中,  , 将
, 将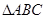 绕点
绕点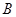 顺时针旋转角
顺时针旋转角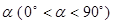 , 得
, 得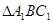 ,
, 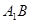 交
交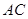 于点
于点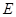 ,
,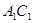 分别交
分别交 于
于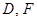 两点.
两点.
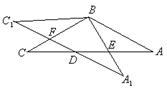
(1) 在旋转过程中, 线段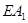 与
与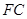 有怎样的数量关系? 证明你的结论;
有怎样的数量关系? 证明你的结论;
(2) 当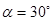 时, 试判断四边形
时, 试判断四边形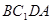 的形状, 并说明理由;
的形状, 并说明理由;
(3) 在(2)的情况下, 求线段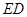 的长.
的长.
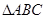 中,
中,  , 将
, 将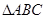 绕点
绕点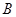 顺时针旋转角
顺时针旋转角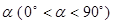 , 得
, 得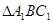 ,
, 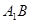 交
交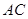 于点
于点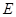 ,
,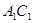 分别交
分别交 于
于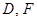 两点.
两点.
(1) 在旋转过程中, 线段
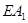 与
与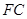 有怎样的数量关系? 证明你的结论;
有怎样的数量关系? 证明你的结论;(2) 当
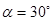 时, 试判断四边形
时, 试判断四边形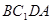 的形状, 并说明理由;
的形状, 并说明理由;(3) 在(2)的情况下, 求线段
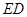 的长.
的长.三角形全等的应用;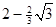
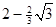
试题分析:(1)
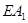 =
=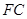 . 由旋转可证明
. 由旋转可证明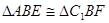 , 或者
, 或者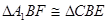 , 所以可得结论;
, 所以可得结论;(2) 四边形
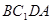 为菱形. 先证四边形
为菱形. 先证四边形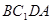 为平行四边形, 再由
为平行四边形, 再由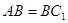 , 所以得菱形;
, 所以得菱形;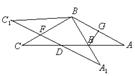
(3) 过点
 作
作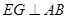 于
于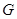 , 在
, 在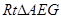 中, 可求得
中, 可求得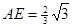 ,
,所以
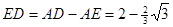 .
.点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目


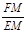 =_______;
=_______;
 角(
角( ),其他条件不变,判断
),其他条件不变,判断
 ,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.




 ,那么它的实际车牌号是: 。
,那么它的实际车牌号是: 。 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线

