题目内容
A,B两地相距60千米,甲骑自行车从A地出发,乙骑摩托车从B地出发相向而行.如果甲比乙早出发1小时40分钟,那么甲出发后3小时与乙相遇,相遇后两人继续前进,当甲到达B地时,乙恰好也到达A地,求甲,乙两人速度.分析:有两个等量关系:甲3小时路程+乙1小时20分路程=60;由于相遇后两人继续前进,当甲到达B地时,乙恰好也到达A地,那么甲后来走乙原先走过的路程的时间=乙后来走甲原先走过的路程的时间,即
=
.
| 甲3小时路程 |
| 乙速度 |
| 乙1小时20分路程 |
| 甲速度 |
解答:解:设甲的速度为x千米/时,乙的速度为y千米/时,则
,
解得
或
(不合题意,舍去).
答:甲的速度为12千米/时,乙的速度为18千米/时.
|
解得
|
|
答:甲的速度为12千米/时,乙的速度为18千米/时.
点评:本题的关键在于弄清题意,找到等量关系.本题需注意2点:两人相遇时各自用的时间;甲后来走乙原先走过的路程的时间=乙后来走甲原先走过的路程的时间.

练习册系列答案
相关题目
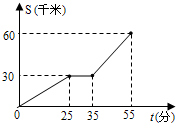 如图反映了一辆汽车从甲地开往乙地的过程中,汽车离开甲地的距离s(千米)与所用时间t(分)之间的函数关系.已知汽车在途中停车加油一次,根据图象,下列描述中,不正确的是( )
如图反映了一辆汽车从甲地开往乙地的过程中,汽车离开甲地的距离s(千米)与所用时间t(分)之间的函数关系.已知汽车在途中停车加油一次,根据图象,下列描述中,不正确的是( )| A、汽车在途中加油用了10分钟 | B、汽车在加油前后,速度没有变化 | C、汽车加油后的速度为每小时90千米 | D、甲乙两地相距60千米 |