题目内容
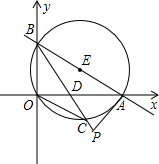 如图,直线y=-
如图,直线y=-
| ||
| 3 |
| 3 |
(1)C是⊙E上一点,连接BC交OA于点D,若∠COD=∠CBO,求点A、B、C的坐标;
(2)求经过O、C、A三点的抛物线的解析式;
(3)若延长BC到P,使DP=2,连接AP,试判断直线PA与⊙E的位置关系,并说明理由.
分析:(1)可根据直线AB的解析式求出A、B两点的坐标,即可得出OB、OA、AB的长,已知了∠COD=∠CBD,那么C就是弧AO的中点,如果连接EC,根据垂径定理可得出EC⊥OA,设垂足为N,那么ON=
OA,而NC可通过EC-EN求得(EN是OB的一半),由此可得出C点坐标;
(2)已知了O、A、C三点坐标,可用待定系数法求出抛物线的解析式;
(3)根据OA、OB的长,不难得出∠ABO=60°,那么∠ABP=∠OBP=30°,因此可得出∠ODB=∠ADP=60°,在直角三角形OBD中,可根据OB的长和∠OBD的正切值求出OD的长,即可求出AD的长为2,因此AD=DP,那么三角形ADP就是等边三角形,在三角形ABP中,∠ABP=30°,∠P=60°,因此∠BAP=90°即可证得PA与圆E相切.
| 1 |
| 2 |
(2)已知了O、A、C三点坐标,可用待定系数法求出抛物线的解析式;
(3)根据OA、OB的长,不难得出∠ABO=60°,那么∠ABP=∠OBP=30°,因此可得出∠ODB=∠ADP=60°,在直角三角形OBD中,可根据OB的长和∠OBD的正切值求出OD的长,即可求出AD的长为2,因此AD=DP,那么三角形ADP就是等边三角形,在三角形ABP中,∠ABP=30°,∠P=60°,因此∠BAP=90°即可证得PA与圆E相切.
解答: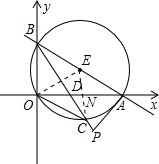 解:(1)连接EC交x轴于点N(如图).
解:(1)连接EC交x轴于点N(如图).
∵A、B是直线y=-
x+
分别与x轴、y轴的交点.
∴A(3,0),B(0,
).
又∵∠COD=∠CBO,
∴∠CBO=∠ABC.
∴C是
的中点,
∴EC⊥OA.
∴ON=
OA=
,EN=
=
.
连接OE.
∴EC=OE=
.
∴NC=EC-EN=
.
∴C点的坐标为(
,-
);
(2)设经过O、C、A三点的抛物线的解析式为y=ax(x-3).
∵C(
,-
),
∴-
=a•
(
-3).
∴a=
.
∴y=
x2-
x为所求;
(3)∵tan∠BAO=
,
∴∠BAO=30°,∠ABO=60°.
由(1)知∠OBD=∠ABD.
∴∠OBD=
∠ABO=
×60°=30°.
∴OD=OB•tan30°=1.
∴DA=2.
∵∠ADC=∠BDO=60°,PD=AD=2.
∴△ADP是等边三角形.
∴∠DAP=60°.
∴∠BAP=∠BAO+∠DAP=30°+60°=90°.
即PA⊥AB.
即直线PA是⊙E的切线.
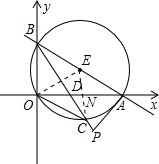 解:(1)连接EC交x轴于点N(如图).
解:(1)连接EC交x轴于点N(如图).∵A、B是直线y=-
| ||
| 3 |
| 3 |
∴A(3,0),B(0,
| 3 |
又∵∠COD=∠CBO,
∴∠CBO=∠ABC.
∴C是
 |
| OA |
∴EC⊥OA.
∴ON=
| 1 |
| 2 |
| 3 |
| 2 |
| OB |
| 2 |
| ||
| 2 |
连接OE.
∴EC=OE=
| 3 |
∴NC=EC-EN=
| ||
| 2 |
∴C点的坐标为(
| 3 |
| 2 |
| ||
| 2 |
(2)设经过O、C、A三点的抛物线的解析式为y=ax(x-3).
∵C(
| 3 |
| 2 |
| ||
| 2 |
∴-
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴a=
2
| ||
| 9 |
∴y=
2
| ||
| 9 |
2
| ||
| 3 |
(3)∵tan∠BAO=
| ||
| 3 |
∴∠BAO=30°,∠ABO=60°.
由(1)知∠OBD=∠ABD.
∴∠OBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD=OB•tan30°=1.
∴DA=2.
∵∠ADC=∠BDO=60°,PD=AD=2.
∴△ADP是等边三角形.
∴∠DAP=60°.
∴∠BAP=∠BAO+∠DAP=30°+60°=90°.
即PA⊥AB.
即直线PA是⊙E的切线.
点评:本题考查了圆周角定理、垂径定理、二次函数解析式的确定、切线的判定等知识.

练习册系列答案
相关题目
 如图,直线y=-
如图,直线y=- 9、如图,直线AB、CD相交于O,∠COE是直角,∠1=57°,则∠2=
9、如图,直线AB、CD相交于O,∠COE是直角,∠1=57°,则∠2= 如图,直线AB的解析式为y=
如图,直线AB的解析式为y= 如图,直线y=x+2与双曲线
如图,直线y=x+2与双曲线 如图,直线AB,CD分别交直线EF于点G,H,AB∥CD,则图中与∠AGE相等的角有
如图,直线AB,CD分别交直线EF于点G,H,AB∥CD,则图中与∠AGE相等的角有