题目内容
13、若直角三角形的两条直角边长分别是6和8,则它的外接圆半径为
5
,内切圆半径为2
.分析:根据直角三角形外接圆的圆心是斜边的中点,由勾股定理求得斜边,设内切圆的半径为r,由切线长定理得6-r+8-r=10,求解即可.
解答: 解:如图,∵AC=8,BC=6,
解:如图,∵AC=8,BC=6,
∴AB=10,
∴外接圆半径为5,
设内切圆的半径为r,
∴CE=CF=r,
∴AD=AF=8-r,BD=BE=6-r,
∴6-r+8-r=10,
解得r=2.
故答案为:5;2.
 解:如图,∵AC=8,BC=6,
解:如图,∵AC=8,BC=6,∴AB=10,
∴外接圆半径为5,
设内切圆的半径为r,
∴CE=CF=r,
∴AD=AF=8-r,BD=BE=6-r,
∴6-r+8-r=10,
解得r=2.
故答案为:5;2.
点评:本题考查了三角形的内切圆和内心,以及外心,注:直角三角形的外心是斜边的中点.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
下列说法正确的是( )
A.若  ,且 ,且 的两条直角边分别是水平和竖直状态,那么 的两条直角边分别是水平和竖直状态,那么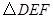 的两条直角边也一定分别是水平和竖直状态 的两条直角边也一定分别是水平和竖直状态 |
B.如果 , , ,那么 ,那么 |
| C.有一条公共边,而且公共边在每个三角形中都是腰的两个等腰三角形一定全等 |
| D.有一条相等的边,而且相等的边在每个三角形中都是底边的两个等腰三角形全等 |

 ,且
,且 的两条直角边分别是水平和竖直状态,那么
的两条直角边分别是水平和竖直状态,那么 的两条直角边也一定分别是水平和竖直状态
的两条直角边也一定分别是水平和竖直状态 ,
, ,那么
,那么