题目内容
已知抛物线y=x2+bx+c经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.
考点:待定系数法求二次函数解析式
专题:计算题
分析:直接把(0,-1),(3,2)代入解析式得到关于b、c的方程组,再解方程组求出b和c即可得到抛物线的解析式,然后配方确定顶点坐标.
解答:解:∵抛物线y=x2+bx+c过(0,-1),(3,2)两点,
∴
,
解得
,
∴抛物线的解析式为y=x2-2x-1,
∵y=x2-2x-1=(x-1)2-2,
∴抛物线的顶点坐标为(1,-2).
∴
|
解得
|
∴抛物线的解析式为y=x2-2x-1,
∵y=x2-2x-1=(x-1)2-2,
∴抛物线的顶点坐标为(1,-2).
点评:本题考查了待定系数法求二次函数关系式:要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在平面直角坐标系xOy中,点P(-3,5)关于y轴的对称点在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
以下列长度的三条线段为边,可以构成三角形的是( )
| A、1,4,7 |
| B、2,5,8 |
| C、3,6,9 |
| D、4,6,8 |
下列长度的三条线段能组成直角三角形的是( )
| A、1,2,3 |
| B、2,3,4 |
| C、3,4,5 |
| D、4,5,6 |
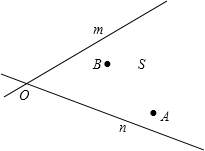 如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹).
如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹). 如图,在一笔直的海岸线上有A、B两个观测站,B在A的正东方向,AB=10千米,在某一时刻,从观测站A测得一艘集装箱货船位于北偏西62.6°的C处,同时观测站B测得改集装箱船位于北偏西69.2°方向,问此时该集装箱船与海岸之间距离CH约多少千米?(最后结果保留整数)
如图,在一笔直的海岸线上有A、B两个观测站,B在A的正东方向,AB=10千米,在某一时刻,从观测站A测得一艘集装箱货船位于北偏西62.6°的C处,同时观测站B测得改集装箱船位于北偏西69.2°方向,问此时该集装箱船与海岸之间距离CH约多少千米?(最后结果保留整数)