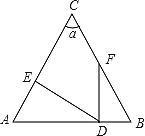
题目内容
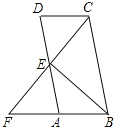
【题目】已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图1,∠BME,∠E,∠END的数量关系为 (直接写出答案);
(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数(用用含m的式子表示)
(3)如图3,点G为CD上一点,∠BMN=n·∠EMN,∠GEK=n·∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)
【答案】(1)∠E=∠BME+∠END;(2)![]() m°;(3)∠GEK=∠BMN+n·∠GEH
m°;(3)∠GEK=∠BMN+n·∠GEH
【解析】试题分析:(1)过点E作l∥AB,利用平行线的性质可得∠1=∠BME,∠2=∠DNE,由∠MEN=∠1+∠2,等量代换可得结论;(2)利用角平分线的性质可得∠NEF=![]() ∠MEN,∠ENP=
∠MEN,∠ENP=![]() ∠END,由EQ∥NP,可得∠QEN=∠ENP=
∠END,由EQ∥NP,可得∠QEN=∠ENP=![]() ∠END,由(1)的结论可得∠MEN=∠BME+∠END,等量代换得出结论;(3)由已知可得∠EMN=
∠END,由(1)的结论可得∠MEN=∠BME+∠END,等量代换得出结论;(3)由已知可得∠EMN=![]() ∠BMN,∠GEM=
∠BMN,∠GEM=![]() ∠GEK,由EH∥MN,可得∠HEM=∠ENM=
∠GEK,由EH∥MN,可得∠HEM=∠ENM=![]() ∠BMN,因为∠GEH=∠GEM-∠HEM,等量代换得出结论.
∠BMN,因为∠GEH=∠GEM-∠HEM,等量代换得出结论.
试题解析:
(1)如图1,过点E作l∥AB,
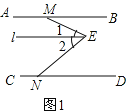
∵AB∥CD,
∴l∥AB∥CD,
∴∠1=∠BME,∠2=∠DNE,
∵∠MEN=∠1+∠2,
∴∠E=∠BME+∠END,
故答案为:∠E=∠BME+∠END;
(2)如图2,
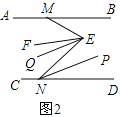
∵EF平分∠MEN,NP平分∠END,
∴∠NEF=![]() ∠MEN,∠ENP=
∠MEN,∠ENP=![]() ∠END,
∠END,
∵EQ∥NP,
∴∠QEN=∠ENP=![]() ∠END,
∠END,
∵∠MEN=∠BME+∠END,
∴∠MEN-∠END=∠BME=m°,
∴∠FEQ=∠NEF-∠NEQ=![]() ∠MEN
∠MEN![]() ∠END=
∠END=![]() (∠MEN∠END)=
(∠MEN∠END)= ![]() m°;
m°;
(3)∠GEK=∠BMN+n∠GEH.
如图3,
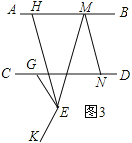
∵∠BMN=n∠EMN,∠GEK=n∠GEK,
∴∠EMN=![]() ∠BMN,∠GEM=
∠BMN,∠GEM=![]() ∠GEK,
∠GEK,
∵EH∥MN,
∴∠HEM=∠ENM=![]() ∠BMN,
∠BMN,
∵∠GEH=∠GEM-∠HEM=![]() ∠GEK
∠GEK![]() ∠BMN,
∠BMN,
∴n∠GEH=∠GEK-∠BMN,
即∠GEK=∠BMN+n∠GEH.

【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
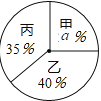
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?