题目内容
【题目】(满分8分)恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷![]() 和世界级自然保护区星斗山
和世界级自然保护区星斗山![]() 位于笔直的沪渝高速公路X同侧,
位于笔直的沪渝高速公路X同侧, ![]() 、
、![]() 到直线x的距离分别为
到直线x的距离分别为![]() 和
和![]() ,要在沪渝高速公路旁修建一服务区
,要在沪渝高速公路旁修建一服务区![]() ,向
,向![]() 、
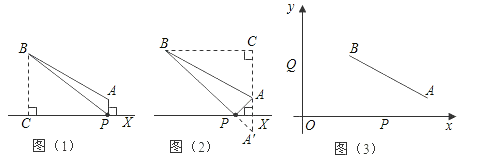
、![]() 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(
两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(![]() 与直线x垂直,垂足为
与直线x垂直,垂足为![]() ),
),![]() 到
到![]() 、
、![]() 的距离之和
的距离之和![]() ,图(2)是方案二的示意图(点
,图(2)是方案二的示意图(点![]() 关于直线x的对称点是
关于直线x的对称点是![]() ,连接
,连接![]() 交直线x于点
交直线x于点![]() ),
),![]() 到
到![]() 、
、![]() 的距离之和
的距离之和![]() .
.
(1)求![]() 、
、![]() ,并比较它们的大小;
,并比较它们的大小;
(2)请你说明![]() 的值为最小;
的值为最小;
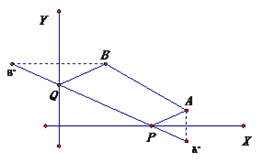
(3)拟建的恩施到张家界高速公路Y与沪渝高速公路垂直,建立如图(3)所示的直角坐标系, ![]() 到直线Y的距离为
到直线Y的距离为![]() ,请你在X旁和Y旁各修建一服务区
,请你在X旁和Y旁各修建一服务区![]() 、
、![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 组成的四边形的周长最小.并求出这个最小值.
组成的四边形的周长最小.并求出这个最小值.
【答案】(1) ![]() ﹥
﹥![]() , (2)
, (2) ![]()
【解析】试题分析:(1)根据勾股定理分别求得S1、S2的值,比较即可;(2)在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA,∴MB+MA=MB+MA'>A'B,∴S2=BA'为最小;(3)过A作关于X轴的对称点A',过B作关于Y轴的对称点B',连接A'B',交X轴于点P,交Y轴于点Q,求出A'B'的值即可.
试题解析:⑴图(1)中过B作BC⊥AP,垂足为C,
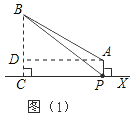
则PC=40,又AP=10,
∴AC=30
在Rt△ABC 中,AB=50 AC=30
∴BC=40
∴ BP=![]()
S1=![]()
图(2)中,过B作BC⊥AA′垂足为C,
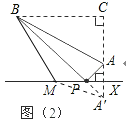
则A′C=50,
又BC=40
∴BA'=![]()
由轴对称知:PA=PA'
∴S2=BA'=![]()
∴![]() ﹥
﹥![]()
(2)如 图10(2),在公路上任找一点M,连接MA,MB,MA',

由轴对称知MA=MA'
∴MB+MA=MB+MA'﹥A'B
∴S2=BA'为最小
(3)过A作关于X轴的对称点A', 过B作关于Y轴的对称点B',连接A'B',交X轴于点P,交Y轴于点Q,则P,Q即为所求,过A'、 B'分别作X轴、Y轴的平行线交于点G,
A'B'=![]()
∴所求四边形的周长为![]()

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案