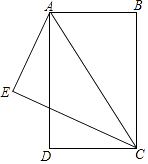
题目内容
【题目】如图，射线AM平行于射线BN，∠B=90°，AB=4，C是射线BN上的一个动点，连接AC，作CD⊥AC，且AC=2CD，过C作CE⊥BN交AD于点E，设BC长为a．
（1）求△ACD的面积（用含a的代数式表示）；
（2）求点D到射线BN的距离（用含有a的代数式表示）；
（3）是否存在点C，使△ACE是以AE为腰的等腰三角形？若存在，请求出此时a的值；若不存在，请说明理由．
【答案】
（1）
解：在Rt△ABC中，AB=4，BC=a，
∴AC= 
= 
，
∴CD= 
AC= 
，
∵∠ACD=90°，
∴S△ACD= ACCD= 
（2）
解：如图1，过点D作DF⊥BN于点F，
∵∠FDC+∠FCD=90°，∠FCD+∠ACB=180°﹣90°=90°，
∴∠FDC=∠ACB，
∵∠B=∠DFC=90°，
∴∠FDC=∠ACB，
∵∠B=∠DFC=90°，
∴△DFC∽△CBA，
∴ 
，
∴DF= BC= a，
∴D到射线BN的距离为 a
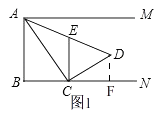
（3）
解：存在，①当EC=EA时，
∵∠ACD=90°，
∴EC=EA= AD，
∵AB∥CE∥DF，
∴BC=FC=a，
由（2）知，△DFC∽△CBA，
∴ 
，
∴FC= AB=2，
∴a=2，
②当AE=AC时，如图2，AM⊥CE，
∴∠1=∠2，
∵AM∥BN，
∴∠2=∠4，
∴∠1=∠4，
由（2）知，∠3=∠4，
∴∠1=∠3，
∵∠AGD=∠DFC=90°，
∴△ADG∽△DCF，
∴ 
，
∵AD= 
= 
，AG=a+2，CD= ，
∴ 
，
∴a=4 
+8，
即：满足条件的a的值为2或4 +8．
【解析】（1）先根据勾股定理得出AC，进而得出CD，最后用三角形的面积公式即可；（2）先判断出∠FDC=∠ACB，进而判断出△DFC∽△CBA，得出 ，即可求出DF，即可；（3）分两种情况利用相似三角形的性质建立方程求解即可得出结论．
【考点精析】本题主要考查了三角形的面积和勾股定理的概念的相关知识点，需要掌握三角形的面积=1/2×底×高；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．
