Question

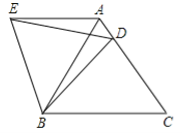
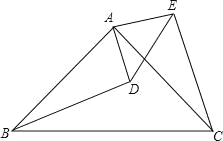
【题目】如图，在△ABC和△ADE中，AC=AB，AE=AD，∠CAB=∠EAD=90°

（1）求证：CE=BD；

（2）求证：CE⊥BD．

Answer 1

【答案】(1)、证明过程见解析；(2)、证明过程见解析.

【解析】

试题分析：(1)、由已知条件证出∠CAE=∠BAD，由SAS证明△CAE≌△BAD，得出对应边相等即可；

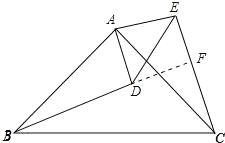
(2)、延长BD交CE于F，由全等三角形的性质得出∠ACE=∠ABD，由角的互余关系得出∠ABC+∠ACB=90°，证出∠DBC+∠BCF=90°，得出∠BFC=90°即可．

试题解析：(1)、∵∠CAB=∠EAD=90°， ∴∠CAE=∠BAD． 在△CAE和△BAD中，

， ∴△CAE≌△BAD（SAS）， ∴CE=BD．

(2)、延长BD交CE于F，如图所示： ∵△CAE≌△BAD， ∴∠ACE=∠ABD， ∵∠CAB=90°，

∴∠ABC+∠ACB=90°， 即∠ABD+∠DBC+∠ACB=90°， ∴∠DBC+∠ACB+∠ACE=90°，

即∠DBC+∠BCF=90°， ∴∠BFC=90°， ∴CE⊥BD．