题目内容
已知:直线y=-
x+
(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2011=
.
| n |
| n+1 |
| ||
| n+1 |
| 2011 |
| 2012 |
| 2011 |
| 2012 |
分析:依次求出S1、S2、Sn,就发现规律:Sn=
,然后求其和即可求得答案.注意
=
-
.
| 1 |
| n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:当n=1时,y=-
x+
,
此时:A(0,
),B(
,0),
则S1=
×
×
=
,
同理:S2=
×
×
×
=
,
…
Sn=
,
故S1+S2+S3+…+S2011=
+
+…+
=1-
+
-
+…+
-
=
;
故答案是:
.
| 1 |
| 2 |
| ||
| 2 |
此时:A(0,
| ||
| 2 |
| 2 |
则S1=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 1×2 |
同理:S2=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2×3 |
…
Sn=
| 1 |
| n(n+1) |
故S1+S2+S3+…+S2011=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2011×2012 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2011 |
| 1 |
| 2012 |
| 2011 |
| 2012 |
故答案是:
| 2011 |
| 2012 |
点评:此题考查了一次函数图象上点的坐标特征.注意发现规律:Sn=
=
-
是解此题的关键.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |

练习册系列答案
相关题目
已知:直线y=-
x+
(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2011=( )
| n |
| n+1 |
| ||
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
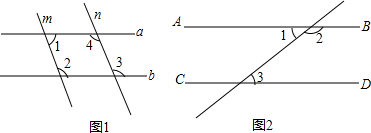 根据题意结合图形填空:
根据题意结合图形填空: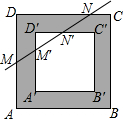 我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为
我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为