Question

【题目】已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．

（1）如图1，求证：△AFB≌△ADC；

（2）请判断图1中四边形BCEF的形状，并说明理由；

（3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．

Answer 1

【答案】（1）见解析（2）四边形BCEF是平行四边形（3）成立

【解析】

试题分析：（1）利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AFB≌△ADC；

（2）四边形BCEF是平行四边形，因为△AFB≌△ADC，所以可得∠ABF=∠C=60°，进而证明∠ABF=∠BAC，则可得到FB∥AC，又BC∥EF，所以四边形BCEF是平行四边形；

（3）易证AF=AD，AB=AC，∠FAD=∠BAC=60°，可得∠FAB=∠DAC，即可证明△AFB≌△ADC；根据△AFB≌△ADC可得∠ABF=∠ADC，进而求得∠AFB=∠EAF，求得BF∥AE，又BC∥EF，从而证得四边形BCEF是平行四边形．

证明：（1）∵△ABC和△ADF都是等边三角形，

∴AF=AD，AB=AC，∠FAD=∠BAC=60°，

又∵∠FAB=∠FAD﹣∠BAD，∠DAC=∠BAC﹣∠BAD，

∴∠FAB=∠DAC，

在△AFB和△ADC中，

，

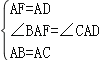∴△AFB≌△ADC（SAS）；

（2）由①得△AFB≌△ADC，

∴∠ABF=∠C=60°．

又∵∠BAC=∠C=60°，

∴∠ABF=∠BAC，

∴FB∥AC，

又∵BC∥EF，

∴四边形BCEF是平行四边形；

（3）成立，理由如下：

∵△ABC和△ADE都是等边三角形，

∴AF=AD，AB=AC，∠FAD=∠BAC=60°，

又∵∠FAB=∠FAD﹣∠BAD，∠DAC=∠BAC﹣∠BAD，

∴∠FAB=∠DAC，

在△AFB和△ADC中，

，

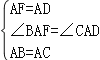∴△AFB≌△ADC（SAS）；

∴∠AFB=∠ADC．

又∵∠ADC+∠DAC=60°，∠EAF+∠DAC=60°，

∴∠ADC=∠EAF，

∴∠AFB=∠EAF，

∴BF∥AE，

又∵BC∥EF，

∴四边形BCEF是平行四边形．