题目内容
 (2013•丰台区一模)我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(-
(2013•丰台区一模)我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(-| 1 |
| 2 |
| 1 |
| 2 |
(1)函数y=x2+4x-5的零点是
-5或1
-5或1
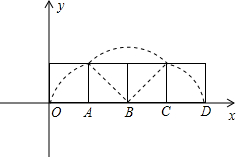
;(2)如图,将边长为1的正方形ABCD放置在平面直角坐标系xOy中,且顶点A在x轴上.若正方形ABCD沿x轴正方向滚动,即先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与x轴所围区域的面积为
π+1
π+1
.分析:(1)将y=0代入y=x2+4x-5,得x2+4x-5=0,解方程求出x的值即为所求;
(2)正方形ABCD沿x轴正方向滚动时,从顶点D落在x轴上的时候开始计算,到下一次D点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,其顶点D从首次落在x轴上和第二次落在x轴上时所画出的轨迹就是函数在其两个相邻零点间的图象,画出图形,不难算出它与x轴所围区域的面积.
(2)正方形ABCD沿x轴正方向滚动时,从顶点D落在x轴上的时候开始计算,到下一次D点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,其顶点D从首次落在x轴上和第二次落在x轴上时所画出的轨迹就是函数在其两个相邻零点间的图象,画出图形,不难算出它与x轴所围区域的面积.
解答:解:(1)∵y=x2+4x-5,
∴当y=0时,x2+4x-5=0,
 解得x=-5或1.
解得x=-5或1.
故答案为-5或1;
(2)考察D点的运动轨迹,D点从x轴上开始运动的时候,首先是围绕A点运动
个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BD为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CD为半径,因此最终构成图象如右所示:
故其与x轴所围成的图形面积为S=
π×12+
×π×(
)2+2×
×1×1=π+1.
故答案为:-5或1;π+1.
∴当y=0时,x2+4x-5=0,
 解得x=-5或1.
解得x=-5或1.故答案为-5或1;
(2)考察D点的运动轨迹,D点从x轴上开始运动的时候,首先是围绕A点运动
| 1 |
| 4 |
故其与x轴所围成的图形面积为S=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 2 |
故答案为:-5或1;π+1.
点评:本题实际上是正方形沿直线无滑动运动时有关顶点的摆线问题,本题考查了函数零点的概念及图形面积的计算,充分考查学生分析问题和解决问题的能力,是一道能力立意的创新题.对于初中生来说,有一定难度.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 (2013•丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=2
(2013•丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=2
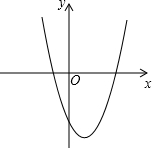 (2013•丰台区一模)二次函数y=x2+bx+c的图象如图所示,其顶点坐标为M(1,-4).
(2013•丰台区一模)二次函数y=x2+bx+c的图象如图所示,其顶点坐标为M(1,-4).
 (2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为
(2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为