题目内容
如图,抛物线 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a= ,点E的坐标是 .
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a= ,点E的坐标是 .
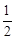 ;(
;(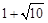 ,
,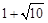 ).
).
解析试题分析:把点A(3,0)代入抛物线 即可求得a的值,正方形OABC可得点C坐标,代入函数解析式求得点D坐标,可知点E横坐标,再利用正方形BDEF的性质得出点E纵坐标问题得解:
即可求得a的值,正方形OABC可得点C坐标,代入函数解析式求得点D坐标,可知点E横坐标,再利用正方形BDEF的性质得出点E纵坐标问题得解:
把点A(3,0)代入抛物线 ,解得a=
,解得a=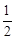 .
.
∵四边形OABC为正方形,∴点C的坐标为(0,3),点D的纵坐标为3.
∵点D在抛物线 上,
上,
∴把y=3代入 解得
解得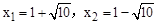 (不合题意,舍去).
(不合题意,舍去).
∴正方形BDEF的边长B为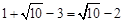 .
.
∴AF=3+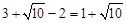 .
.
∴点E的坐标为(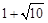 ,
,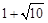 ).
).
考点:1.曲线上点的坐标与方程的关系;2. 正方形的性质,3.解一元二次方程.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 取最大值时,x= .
取最大值时,x= . 的图象经过原点,则m= .
的图象经过原点,则m= . 与抛物线
与抛物线 交于点P,P点的纵坐标为-1,则关于x的方程
交于点P,P点的纵坐标为-1,则关于x的方程 的解是 .
的解是 .
 (
( )与
)与 轴的两个交点分别为
轴的两个交点分别为 和
和 ,当
,当 时,
时,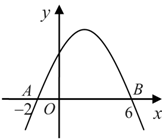
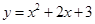 绕着它与y轴的交点旋转180°,所得抛物线的解析式为 .
绕着它与y轴的交点旋转180°,所得抛物线的解析式为 . 、F
、F 在抛物线
在抛物线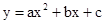 的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
 的数量关系式为:S=
的数量关系式为:S= 
 x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣
x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣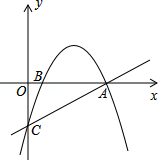
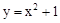 的最小值是 .
的最小值是 .