题目内容
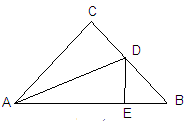
如图:在△ABC中,AB=3㎝,AC=4㎝,则BC边上的中线AD的取值范围是 ;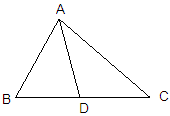

0.5cm<AD<3.5cm
试题分析:延长AD到E,使AD=DE,连接CE,则可得△ABD≌△ECD,得到AB=CE,在△ACE中,根据三角形的三边关系,即可得到结果.
延长AD到E,使AD=DE,连接CE,
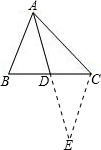
∵AD是△ABC中BC边上的中线,
∴BD=CD,又AD=DE,∠ADB=∠CDE,
∴△ABD≌△ECD,
∴AB=CE,
在△ACE中,AC-CE<AE<AC+CE,即AC-AB<AE<AC+AB,
4-3<AE<4+3,即1<AE<7,
∴0.5cm<AD<3.5cm.
点评:解答本题的关键是熟练掌握三角形的三边关系:任两边之和大于第三边,任两边之差小于第三边.

练习册系列答案
相关题目

 .
.