题目内容
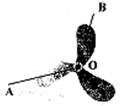
如图,在△ABC中,∠ABC=90°,AB=BC,BD为斜边AC上的中线,将△ABD绕点D顺时针旋转α(0°<α<180°),得到△EFD,点A的对应顶点是E,点B的对应顶点是F,连接BE、CF。试判断BE与CF的长度是否相等,并说明理由。


BE=CF,理由见解析.
试题分析:根据已知条件得出BD=AD=CD.∠ADB=∠BDC=90°,再根据△ABD旋转得到△EFD,得出∠EDB=∠FDC,从而证出△BED≌△CFD,得出BE=CF.
试题解析:BE与CF的长度相等,理由如下:
∵∠ABC=90°,BD为斜边AC的中线,AB=BC,
∴BD=AD=CD.∠ADB=∠BDC=90°.
∵△ABD旋转得到△EFD,
∴∠EDB=∠FDC.
在△BED和△CFD中,
 ,
,∴△BED≌△CFD.
∴BE=CF.
考点: 1.旋转的性质;2.直角三角形斜边上的中线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
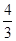 ,如果将△ABC沿直线l翻折后,
,如果将△ABC沿直线l翻折后,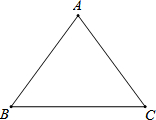
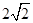 ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).