��Ŀ����
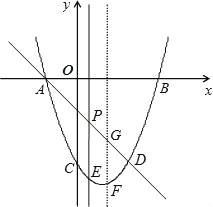
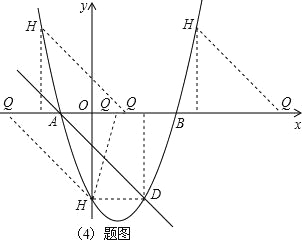
����Ŀ����ͼ��ֱ��AD��Ӧ�ĺ�����ϵʽΪy=��x��1���������߽��ڵ�A����x���ϣ�����D����������x����һ����ΪB��3��0������������y�ύ��C��0����3����
��1���������ߵĽ���ʽ��
��2��P���߶�AD�ϵ�һ�����㣬��P����y���ƽ���߽���������E�㣬���߶�PE���ȵ����ֵ��
��3������F�������ߵĶ��㣬��G��ֱ��AD�������߶Գ���Ľ��㣬���߶�AD���Ƿ����һ��P��ʹ���ı���GFEPΪƽ���ı��Σ�
��4����H�������ϵĶ��㣬��x�����Ƿ���ڵ�Q��ʹA��D��H��Q���ĸ���Ϊ������ı�����ƽ���ı��Σ�������ڣ�ֱ��д����������������Q�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1�������߽���ʽΪy=x2��2x��3��
��2����x=![]() ʱ��PE�����ֵ�����ֵΪ
ʱ��PE�����ֵ�����ֵΪ![]() ��
��
��3�����ڵ�P��0����1����ʹ���ı���GFEPΪƽ���ı��Σ�
��4�����ڵ�Q����3��0����1��0����4��![]() ��0����4+
��0����4+![]() ��0����ʹA��D��H��Q���ĸ���Ϊ������ı�����ƽ���ı��Σ�
��0����ʹA��D��H��Q���ĸ���Ϊ������ı�����ƽ���ı��Σ�
��������
�����������1���ȸ���ֱ�߽���ʽ�����A�����꣬�����ô���ϵ��������κ�������ʽ���㼴�ɵý⣻
��2������ֱ�߽���ʽ��ʾ����P�����꣬���������߽���ʽ��ʾ����E�����꣬���õ�P���������ȥ��E�������꣬�������ɵõ�PE�ı���ʽ��������ֱ�߽���ʽ�������߽���ʽ�����D�����꣬�õ���P�ĺ������ȡֵ��Χ��Ȼ����ݶ��κ�������ֵ������
��3���������ߵĽ���ʽת��Ϊ����ʽ��Ȼ�������F�����꣬�����öԳ�����ݵ�P��ֱ���������G�����꣬Ȼ�����ƽ���ı��εĶԱ�ƽ���������ʽ�ⷽ�̼����жϲ������P�����ꣻ
��4��������H��x���·�ʱ������ƽ���ı��εĶԱ�ƽ������ȣ��ɵõ�H�����������D����������ȣ�Ȼ����������߽���ʽ�����H�ĺ����꣬�����HD�ij��ȣ�Ȼ��ֵ�Q�ڵ�A��������ұ�������������Q�����ꣻ
������H��x���Ϸ�ʱ��AQֻ����ƽ���ı��εĶԽ��ߣ����ݵ�D������õ���H�������꣬Ȼ����������߽���ʽ�����H�ĺ����꣬Ȼ����ݵ�H�ĺ������ʾ�ĵ㵽��Q�ľ�����ڵ�D�ĺ������ʾ�ĵ㵽��A�ľ��������⼴�ɣ�
�����������1����y=0������x��1=0�����x=��1�����ԣ���A������Ϊ����1��0����
�������߽���ʽΪy=ax2+bx+c����B��3��0����C��0����3�����������ϣ���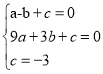 �����
�����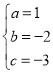 �����ԣ������߽���ʽΪy=x2��2x��3��
�����ԣ������߽���ʽΪy=x2��2x��3��
��2����P���߶�AD�ϵ�һ�����㣬��P����y���ƽ���߽���������E�㣬
�����P��x����x��1�������E��������x��x2��2x��3����
PE=����x��1������x2��2x��3����
=��x��1��x2+2x+3��
=��x2+x+2��
=����x��![]() ��2+
��2+![]() ������
������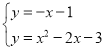 �����
�����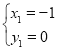 ��
��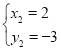 ��
��
���ԣ���D������Ϊ��2����3����
��P���߶�AD�ϵ�һ�����㣬
�ੁ1��x��2��
����x=![]() ʱ��PE�����ֵ�����ֵΪ
ʱ��PE�����ֵ�����ֵΪ![]() ��
��
��3����y=x2��2x��3=��x��1��2��4��
����F������Ϊ��1����4������G�ĺ�����Ϊ1��
y=��1��1=��2��
����G����������1����2����
��GF=��2������4��=��2+4=2��
���ı���GFEPΪƽ���ı��Σ�
��PE=GF��
�ੁx2+x+2=2��
���x1=0��x2=1����ȥ����
��ʱ��y=��1��
����P��������0����1����
�ʣ����ڵ�P��0����1����ʹ���ı���GFEPΪƽ���ı��Σ�
��4�����ڣ��������£�
������H��x���·�ʱ������Q��x���ϣ�
��HD��AQ��
����H�����������D��ͬ������3��
��ʱ��x2��2x��3=��3��
�����ã�x2��2x=0��
���x1=0��x2=2����ȥ����
��HD=2��0=2��
����A����������1��0����
��1��2=��3����1+2=1��
����Q����������3��0����1��0����
������H��x���Ϸ�ʱ������ƽ���ı��εĶԳ��ԣ���H��AQ�ľ�����ڵ�D��AQ�ľ��룬
����D��������Ϊ��3������H��������Ϊ3����x2��2x��3=3��
�����ã�x2��2x��6=0��
���x1=1��![]() ��x2=1+
��x2=1+![]() ��
��
����A�ĺ�����Ϊ��1����D�ĺ�����Ϊ2��
2������1��=2+1=3��
����ƽ���ı��ε����ʣ�1��![]() +3=4��
+3=4��![]() ��1+
��1+![]() +3=4+
+3=4+![]() ��
��
����Q��������4��![]() ��0����4+
��0����4+![]() ��0����
��0����
�������������ڵ�Q����3��0����1��0����4��![]() ��0����4+
��0����4+![]() ��0����ʹA��D��H��Q���ĸ���Ϊ������ı�����ƽ���ı��Σ�
��0����ʹA��D��H��Q���ĸ���Ϊ������ı�����ƽ���ı��Σ�

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij��������10����������ͳ�����±�����õ�����10��������µ������ǣ� ��
�������(��C) | 18 | 19 | 20 | 21 | 22 |
���� | 1 | 2 | 2 | 3 | 2 |
A.20B.20.5C.21D.22