题目内容
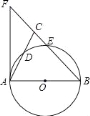
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
【答案】(1)见解析;
(2)CE=2.
【解析】
试题分析:(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)首先连接AE,设CE=x,由勾股定理可得方程:(2![]() )2=x2+(3x)2求得答案.
)2=x2+(3x)2求得答案.
试题解析:(1)证明:如图,连接BD.∵AB为⊙O的直径,∴∠ADB=90°,∴∠DAB+∠ABD=90°.∵AF是⊙O的切线,∴∠FAB=90°,即∠DAB+∠CAF=90°.∴∠CAF=∠ABD.∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.∴∠ABC=2∠CAF.
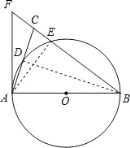
(2)如图,连接AE,∴∠AEB=90°,设CE=x,∵CE:EB=1:4,
∴EB=4x,BA=BC=5x,AE=3x,在Rt△ACE中,AC2=CE2+AE2,
即(2![]() )2=x2+(3x)2,∴x=2.∴CE=2.
)2=x2+(3x)2,∴x=2.∴CE=2.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目