题目内容
【题目】正方形ABCD中,点P为直线AB上一个动点(不与点A,B重合),连接DP,将DP绕点P旋转90°得到EP,连接DE,过点E作CD的垂线,交射线DC于M,交射线AB于N.
问题出现:(1)当点P在线段AB上时,如图1,线段AD,AP,DM之间的数量关系为 ;
题探究:(2)①当点P在线段BA的延长线上时,如图2,线段AD,AP,DM之间的数量关系为 ;
②当点P在线段AB的延长线上时,如图3,请写出线段AD,AP,DM之间的数量关系并证明;
问题拓展:(3)在(1)(2)的条件下,若AP=![]() ,∠DEM=15°,则DM= .
,∠DEM=15°,则DM= .

【答案】(1) DM=AD+AP ;(2) ①DM=AD﹣AP ; ②DM=AP﹣AD ;(3) 3﹣![]() 或
或![]() ﹣1.
﹣1.
【解析】
(1)根据正方形的性质和全等三角形的判定和性质得出△ADP≌△PFN,进而解答即可;
(2)①根据正方形的性质和全等三角形的判定和性质得出△ADP≌△PFN,进而解答即可;
②根据正方形的性质和全等三角形的判定和性质得出△ADP≌△PFN,进而解答即可;
(3)分两种情况利用勾股定理和三角函数解答即可.
(1)DM=AD+AP,理由如下:
∵正方形ABCD,
∴DC=AB,∠DAP=90°,
∵将DP绕点P旋转90°得到EP,连接DE,过点E作CD的垂线,交射线DC于M,交射线AB于N,
∴DP=PE,∠PNE=90°,∠DPE=90°,
∵∠ADP+∠DPA=90°,∠DPA+∠EPN=90°,
∴∠DAP=∠EPN,
在△ADP与△NPE中,
 ,
,
∴△ADP≌△NPE(AAS),
∴AD=PN,AP=EN,
∴AN=DM=AP+PN=AD+AP;
(2)①DM=AD﹣AP,理由如下:
∵正方形ABCD,
∴DC=AB,∠DAP=90°,
∵将DP绕点P旋转90°得到EP,连接DE,过点E作CD的垂线,交射线DC于M,交射线AB于N,
∴DP=PE,∠PNE=90°,∠DPE=90°,
∵∠ADP+∠DPA=90°,∠DPA+∠EPN=90°,
∴∠DAP=∠EPN,
在△ADP与△NPE中,
 ,
,
∴△ADP≌△NPE(AAS),
∴AD=PN,AP=EN,
∴AN=DM=PN﹣AP=AD﹣AP;
②DM=AP﹣AD,理由如下:
∵∠DAP+∠EPN=90°,∠EPN+∠PEN=90°,
∴∠DAP=∠PEN,
又∵∠A=∠PNE=90°,DP=PE,
∴△DAP≌△PEN,
∴AD=PN,
∴DM=AN=AP﹣PN=AP﹣AD;
(3)有两种情况,如图2,DM=3﹣![]() ,如图3,DM=
,如图3,DM=![]() ﹣1;
﹣1;
①如图2:∵∠DEM=15°,
∴∠PDA=∠PDE﹣∠ADE=45°﹣15°=30°,
在Rt△PAD中AP=![]() ,AD=
,AD=![]() =3,
=3,
∴DM=AD﹣AP=3﹣![]() ;
;
②如图3:∵∠DEM=15°,
∴∠PDA=∠PDE﹣∠ADE=45°﹣15°=30°,
在Rt△PAD中AP=![]() ,AD=APtan30°=
,AD=APtan30°=![]() =1,
=1,
∴DM=AP﹣AD=![]() ﹣1.
﹣1.
故答案为;DM=AD+AP;DM=AD﹣AP;3﹣![]() 或
或![]() ﹣1.
﹣1.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】某年级共有300名学生,为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制)、并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
a.A课程成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100);
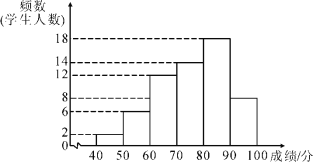
b.A课程成绩在70≤x<80这一组的是:
70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
c.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A | 75.8 | m | 84.5 |
B | 72.2 | 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是______(填“A”或“B”),理由是________________________________;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过75.8分的人数.




