题目内容
一次函数y=mx+2与正比例函数y=2mx(m为常数,且m≠0)在同一坐标系中的图象的是
- A.
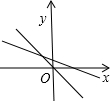
- B.
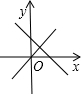
- C.
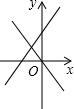
- D.

A
分析:因为m的符号不明确,所以应分两种情况讨论,找出符合任意条件的选项即可.
解答:分两种情况:
1、当m>0时,一次函数y=mx+2经过第一、二、三象限;正比例函数y=2mx过原点、第一、三象限,无选项符合;
2、当m<0时,一次函数y=mx+2经过第一、二、四象限;正比例函数y=2mx过原点、第二、四象限,选项A符合.
故选A.
点评:正比例函数y=kx(k≠0)的图象是过原点的一条直线:
k<0,正比例函数的图象过原点、第二、四象限;
k>0,正比例函数的图象过原点、第一、三象限.
一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
分析:因为m的符号不明确,所以应分两种情况讨论,找出符合任意条件的选项即可.
解答:分两种情况:
1、当m>0时,一次函数y=mx+2经过第一、二、三象限;正比例函数y=2mx过原点、第一、三象限,无选项符合;
2、当m<0时,一次函数y=mx+2经过第一、二、四象限;正比例函数y=2mx过原点、第二、四象限,选项A符合.
故选A.
点评:正比例函数y=kx(k≠0)的图象是过原点的一条直线:
k<0,正比例函数的图象过原点、第二、四象限;
k>0,正比例函数的图象过原点、第一、三象限.
一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.

练习册系列答案
相关题目
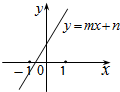 13、一次函数y=mx+n的图象如图所示,则代数式|m+n|-|m-n|化简后的结果为
13、一次函数y=mx+n的图象如图所示,则代数式|m+n|-|m-n|化简后的结果为