题目内容
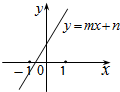 13、一次函数y=mx+n的图象如图所示,则代数式|m+n|-|m-n|化简后的结果为
13、一次函数y=mx+n的图象如图所示,则代数式|m+n|-|m-n|化简后的结果为
2n
.分析:根据一次函数图象的特点确定m-n的符号,代入原式计算即可.
解答:解:由一次函数的性质可知,m>0,n>0,即m+n>0;
且当x=-1时,y<0,即-m+n<0,
∴m-n>0.
所以|m+n|-|m-n|=m+n-(m-n)=2n.
且当x=-1时,y<0,即-m+n<0,
∴m-n>0.
所以|m+n|-|m-n|=m+n-(m-n)=2n.
点评:主要考查一次函数的性质和绝对值性质,要会从图象上找到所需要的相等关系或不等关系.然后再把绝对值符号去掉.解此类题的关键是:先利用条件判断出绝对值符号里代数式的正负性,再根据绝对值的性质把绝对值符号去掉,把式子化简,即可求解.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目