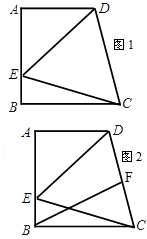
题目内容
已知：如图，梯形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．
（1）求证：△ABE≌△FCE；
（2）若BC⊥AB，且BC=16，AB=15，求AF的长．
（1）求证：△ABE≌△FCE；
（2）若BC⊥AB，且BC=16，AB=15，求AF的长．
（1）证明：∵E为BC的中点，
∴BE=CE，
∵AB∥CD，
∴∠BAE=∠F，∠B=∠FCE，
∴△ABE≌△FCE；（4分）
（2）由（1）可得△ABE≌△FCE，
∴CF=AB=15，CE=BE=8，AE=EF，
∵∠B=∠BCF=90°，
根据勾股定理，得AE=17，
∴AF=34．（8分）
∴BE=CE，
∵AB∥CD，
∴∠BAE=∠F，∠B=∠FCE，
∴△ABE≌△FCE；（4分）
（2）由（1）可得△ABE≌△FCE，
∴CF=AB=15，CE=BE=8，AE=EF，
∵∠B=∠BCF=90°，
根据勾股定理，得AE=17，
∴AF=34．（8分）
练习册系列答案
阅读快车系列答案
相关题目
