题目内容
【题目】如图,弦BE与弦CD交于点G,点E为 ![]() 的中点,过点B的直线交DC延长线于点A,AB∥DE.
的中点,过点B的直线交DC延长线于点A,AB∥DE.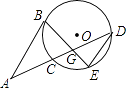
(1)若AB=AG,求证:AB是⊙O切线;
(2)在(1)条件下,若tanA= ![]() ,DE=10,求⊙O的半径.
,DE=10,求⊙O的半径.
(3)求证:AG2﹣BG2=ACAG.
【答案】
(1)证明:如图1中,连接OB、OE交AD于F.
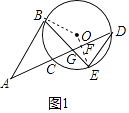
∵ ![]() =
= ![]() ,
,
∴OE⊥CD,
∴∠EFG=90°,
∴∠GEF+∠EGF=90°,
∵AB=AG,
∴∠ABG=∠AGB=∠EGF,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠ABG+∠OBE=90°,
∴∠ABO=90°
∴AB是⊙O的切线.
(2)解:如图2中,连接OD.
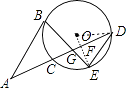
∵AB∥DE,
∴∠A=∠ADE,
在Rt△DFE中,tan∠DFE= ![]() =
= ![]() ,设EF=3k,DF=4k,则DE=5k,
,设EF=3k,DF=4k,则DE=5k,
由题意DE=10,
∴5k=10,
∴k=2,
∴EF=6,DF=8,
设⊙O的半径为r,
在Rt△ODF中,∵OD2=OF2+DF2,
∴r2=(r﹣6)2+82,
∴r= ![]() .
.
(3)证明:如图3中,连接BC.
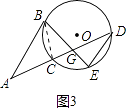
∵AB∥DE,
∴∠A=∠ADE,
∵∠CBG=∠ADE,
∴∠CBG=∠A,∵∠BGC=∠AGB,
∴△BGC∽△AGB,
∴ ![]() =
= ![]() ,
,
∴BG2=AGCG,
∴AG2﹣BG2=AG2﹣AGCG=AG(AG﹣CG)=AGAC.
【解析】(1)连接OB、OE交AD于F.首先依据垂径定理的推理可得到∠EFG=90°,则∠GEF+∠EGF=90°,接下来,再证明∠ABG=∠EGF,∠OBE=∠OEB,依据等式的性质可证明∠ABG+∠OBE=90°,最后依据切线的判定定理进行证明即可;
(2)连接OD.在Rt△DFE中,设EF=3k,DF=4k,依据勾股定理可知DE=5k,由题意DE=10,可得k=2,推出EF=6,DF=8,设⊙O的半径为r,在Rt△ODF中,根据OD2=OF2+DF2列出关于r的方程求解即可;
(3)连接BC.首先证明△BGC∽△AGB,依据相似三角形的性质可得到BG2=AGCG,将BG2=AGCG代入变形即可.