题目内容

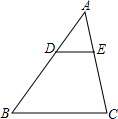（2014•静安区一模）如图，已知在△ABC中，点D、E分别在边AB、AC上，DE∥BC，
AD
DB
=
2
3
，如果
AB
=
a
，
BC
=
b
．
（1）求
EA
（用向量
a
，
b
的式子表示）
（2）求作向量
1
2
a
-
b
（不要求写作法，但要指出所作图表中表示结论的向量）
分析：（1）由DE∥BC，
AD
DB
=
2
3
，根据平行线分线段成比例定理，可求得AE：AC=2：5，又由
AB
=
a
，
BC
=
b
，利用三角形法则，即可求得
AC
，继而求得答案；
（2）取点AB的中点M，作
NB
=
BC
，连接
MN
，则
MN
即为所求．
解答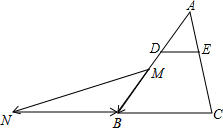：解：（1）∵DE∥BC，
∴
AE
AC
=
AD
AB
=
2
5
，
∵
AB
=
a
，
BC
=
b
，
∴
AC
=
AB
+
BC
=
a
+
b
，
∴
EC
=
2
5
AC
=
2
5
（
a
+
b
）=
2
5
a
+
2
5
b
；

（2）如图，取点AB的中点M，作
NB
=
BC
，连接
MN
，则
MN
即为所求．
点评：此题考查了平面向量的知识．此题难度适中，注意掌握三角形法则的应用，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
（2014•静安区一模）如果抛物线y=mx2+（m-3）x-m+2经过原点，那么m的值等于（　　）
（2014•静安区一模）如图，已知平行四边形ABCD中，向量
BD
在
BA
，
BC
方向上的分量分别是（　　）
（2014•静安区一模）抛物线y=-（x-2）2+1经过平移后与抛物线y=-（x+1）2-2重合，那么平移的方法可以是（　　）
（2014•静安区一模）在△ABC，点D、E分别在边AB、AC上，如果AD=1，BD=2，那么由下列条件能够判定DE∥BC的是（　　）
（2014•静安区一模）如图，已知AB、CD分别表示两幢相距30米的大楼，小明在大楼底部点B处观察，当仰角增大到30度时，恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像，那么大楼AB的高度为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网